题目内容
6.命题p:关于x的不等式mx2+1>0的解集是R,命题q:函数f(x)=logmx是减函数,若p∧q为真,p∨q为假,则实数m的取值范围是m>1.分析 对于命题p:利用一元二次不等式的解集与判别式的关系可得p的范围;对于命题q:利用对数函数的单调性即可得出.若p∧q为真,p∨q为假,则p与q必然一真一假.
解答 解:命题p:关于x的不等式mx2+1>0的解集是R,m=0时成立;m≠0时,$\left\{\begin{array}{l}{m>0}\\{△=0-4m<0}\end{array}\right.$,解得m>0,∴m≥0.
命题q:函数f(x)=logmx是减函数,∴0<m<1.
若p∧q为真,p∨q为假,
则p与q必然一真一假,
∴$\left\{\begin{array}{l}{m≥0}\\{m>1}\end{array}\right.$,或$\left\{\begin{array}{l}{m<0}\\{0<m<1}\end{array}\right.$,
解得m>1或m∈∅.
则实数m的取值范围m>1.
故答案为:m>1.
点评 本题考查了一元二次不等式的解集与判别式的关系、对数函数的单调性、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.如图E,F在边长分别为2和1的矩形边DC与BC上,若$\overrightarrow{AE}•\overrightarrow{AF}$=6,则$\overrightarrow{BE}•(\overrightarrow{DF}+\overrightarrow{AF})$等于( )
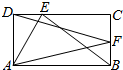

| A. | 3 | B. | 2 | C. | 1 | D. | $\frac{1}{2}$ |
16.在三棱锥P一ABC中,PA⊥平面ABC,△ABC为边长为2的正三角形,PA=$\sqrt{3}$,则AP与平面PBC所成的角为( )
| A. | 45° | B. | 60° | C. | 75° | D. | 90° |
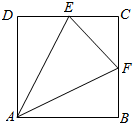 如图,正方形ABCD中,E、F分别为CD、BC的中点,沿AE、AF、EF将其折成一个多面体,则此多面体是直三棱锥.
如图,正方形ABCD中,E、F分别为CD、BC的中点,沿AE、AF、EF将其折成一个多面体,则此多面体是直三棱锥.