题目内容
5.设单位向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|3$\overrightarrow{a}$+$\overrightarrow{b}$|=2$\sqrt{3}$,则|3$\overrightarrow{a}$-$\overrightarrow{b}$|=( )| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
分析 根据向量的模,先把|3$\overrightarrow{a}$+$\overrightarrow{b}$|=2$\sqrt{3}$两边平方,得到6$\overrightarrow{a}•\overrightarrow{b}$=2,求出|$\overrightarrow{a}$-3$\overrightarrow{b}$|2,问题即可解决.
解答 解:∵|3$\overrightarrow{a}$+$\overrightarrow{b}$|=2$\sqrt{3}$,
∴|3$\overrightarrow{a}$+$\overrightarrow{b}$|2=(2$\sqrt{3}$)2,
∴|3$\overrightarrow{a}$|2+|$\overrightarrow{b}$|2+6$\overrightarrow{a}•\overrightarrow{b}$=12,
∴6$\overrightarrow{a}•\overrightarrow{b}$=12-|3$\overrightarrow{a}$|2-|$\overrightarrow{b}$|2=12-9-1=2
|3$\overrightarrow{a}$-$\overrightarrow{b}$|2=|3$\overrightarrow{a}$|2+|$\overrightarrow{b}$|2-6$\overrightarrow{a}•\overrightarrow{b}$=9+1-2=8
∴|$\overrightarrow{a}$-3$\overrightarrow{b}$|=2$\sqrt{2}$
故选:A
点评 本题主要考察了向量模的求解,关键掌握公式的灵活应用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
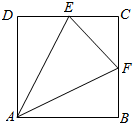 如图,正方形ABCD中,E、F分别为CD、BC的中点,沿AE、AF、EF将其折成一个多面体,则此多面体是直三棱锥.
如图,正方形ABCD中,E、F分别为CD、BC的中点,沿AE、AF、EF将其折成一个多面体,则此多面体是直三棱锥.