Question

19．已知F是椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的右焦点，点P在椭圆C上，线段PF与圆${（x-\frac{c}{3}）^2}+{y^2}=\frac{b^2}{9}$相切于点Q，且PQ=2QF，则椭圆C的离心率等于（　　）

• A． $\frac{{\sqrt{5}}}{3}$
• B． $\frac{2}{3}$
• C． $\frac{{\sqrt{2}}}{2}$
• D． $\frac{1}{2}$

Answer 1

分析 设椭圆的左焦点为F₁，确定PF₁⊥PF，|PF₁|=b，|PF|=2a-b，即可求得a=$\frac{3}{2}$b，根据椭圆的离心率即可得到所求．

解答 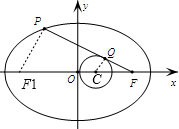解：设椭圆的左焦点为F₁，连接F₁，设圆心为C，则
∵${（x-\frac{c}{3}）^2}+{y^2}=\frac{b^2}{9}$，则圆心坐标为（$\frac{c}{3}$，0），半径为r=$\frac{b}{3}$，
∴|F₁F|=3|FC|
∵PQ=2QF，∴PF₁∥QC，|PF₁|=b
∴|PF|=2a-b
∵线段PF与圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$（其中c²=a²-b²）相切于点Q，
∴CQ⊥PF
∴PF₁⊥PF
∴b²+（2a-b）²=4c²
∴b²+（2a-b）²=4（a²-b²）
∴a=$\frac{3}{2}$b，则$\frac{b}{a}$=$\frac{2}{3}$，
∴e=$\frac{c}{a}$=$\sqrt{1-\frac{{b}^{2}}{{a}^{2}}}$=$\frac{\sqrt{5}}{3}$，
故选A．

点评 本题考查椭圆的几何性质，考查直线与圆的位置关系，确定几何量的关系是关键，属于中档题．