题目内容
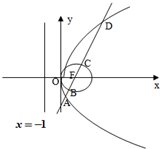
 在平面直角坐标系中,已知定圆F:(x-1)2+y2=1(F为圆心),定直线l:x=-2,作与圆F内切且和直线l相切的动圆P,
在平面直角坐标系中,已知定圆F:(x-1)2+y2=1(F为圆心),定直线l:x=-2,作与圆F内切且和直线l相切的动圆P,(1)试求动圆圆心P的轨迹E的方程.
(2)设过定圆心F的直线m自下而上依次交轨迹E及定园F于点A、B、C、D,
①是否存在直线m,使得|AD|=2|BC|成立?若存在,请求出这条直线的方程;若不存在,请说明理由.
②当直线m绕点F转动时,|AB|•|CD|的值是否为定值?若是,请求出这个定值;若不是,请说明理由.
考点:轨迹方程,直线与圆的位置关系,直线与圆锥曲线的关系
专题:圆锥曲线的定义、性质与方程
分析:(1)设动圆心P(x,y),利用动圆P与定园F内切,列出方程,然后化简求出轨迹方程.
(2)①当直线m的斜率存在,联立
设A(x1,y1),D(x2,y2),利用韦达定理求出|AD|,利用|AD|=2|BC|,求出k即可.然后求出直线方程.
②当直线m的斜率存在时,利用①|AB|•|CD|=(|AF|-1)•(|DF|-1)=x1•x2=1,说明对于任意的直线m,|AB|•|CD|=1为定值.
(2)①当直线m的斜率存在,联立
|
②当直线m的斜率存在时,利用①|AB|•|CD|=(|AF|-1)•(|DF|-1)=x1•x2=1,说明对于任意的直线m,|AB|•|CD|=1为定值.
解答:
 解:(1)设动圆心P(x,y)
解:(1)设动圆心P(x,y)
因为动圆P与定园F内切,则
=|x+2|-1
若x≥-2,则
=x+1⇒y2=4x,
若x<-2,则
=-x-3⇒y2=8(x+1),与x<-2矛盾.
故动圆心P的轨迹是以F为焦点,x=-1为准线的抛物线,
其方程为:y2=4x.…(4分)
(2)①当直线m的斜率存在,由
⇒k2x2-(2k2+4)x+k2=0
设A(x1,y1),D(x2,y2),则x1+x2=2+
,
•x2=1,∴|AD|=|AF|+|DF|=x1+1+x2+1=4+
,而|BC|=2,
若|AD|=2|BC|,则4+
=4,k无解,此时不存在.…(8分)
当直线m的斜率不存在时,则|AD|=4,|BC|=2,显然|AD|=2|BC|成立.
故存在直线m使|AD|=2|BC|成立.此时直线m:x=1.…(9分)
②当直线m的斜率存在时,由①|AB|•|CD|=(|AF|-1)•(|DF|-1)=x1•x2=1
当直线m的斜率不存在时,|AB|•|CD|=(|AF|-1)•(|DF|-1)=(2-1)(2-1)=1.
故对于任意的直线m,|AB|•|CD|=1为定值.…(13分)
 解:(1)设动圆心P(x,y)
解:(1)设动圆心P(x,y)因为动圆P与定园F内切,则
| (x-1)2+y2 |
若x≥-2,则
| (x-1)2+y2 |
若x<-2,则
| (x-1)2+y2 |
故动圆心P的轨迹是以F为焦点,x=-1为准线的抛物线,
其方程为:y2=4x.…(4分)
(2)①当直线m的斜率存在,由
|
设A(x1,y1),D(x2,y2),则x1+x2=2+
| 4 |
| k2 |
| x | 1 |
| 4 |
| k2 |
若|AD|=2|BC|,则4+
| 4 |
| k2 |
当直线m的斜率不存在时,则|AD|=4,|BC|=2,显然|AD|=2|BC|成立.
故存在直线m使|AD|=2|BC|成立.此时直线m:x=1.…(9分)
②当直线m的斜率存在时,由①|AB|•|CD|=(|AF|-1)•(|DF|-1)=x1•x2=1
当直线m的斜率不存在时,|AB|•|CD|=(|AF|-1)•(|DF|-1)=(2-1)(2-1)=1.
故对于任意的直线m,|AB|•|CD|=1为定值.…(13分)
点评:本题考查轨迹方程的求法,直线与抛物线的位置关系的综合应用,考查分析问题解决问题的能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
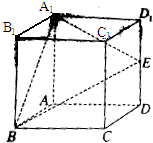 如图,正方体ABCD-A1B1C1D1中,E是棱DD1的中点,F是侧面CDD1C1上的动点,且B1F∥平面A1BE,则B1F与平面CDD1C1所成角的正弦值构成的集合是 ( )
如图,正方体ABCD-A1B1C1D1中,E是棱DD1的中点,F是侧面CDD1C1上的动点,且B1F∥平面A1BE,则B1F与平面CDD1C1所成角的正弦值构成的集合是 ( )| A、{2} | ||||||||
B、
| ||||||||
C、{t|
| ||||||||
D、{t|
|
将函数f(x)=3sin(2x+
)-1的图形按向量
=(m,n)平移后得到函数g(x)=3sin2x的图形则向量
的一个可能值是( )
| π |
| 3 |
| a |
| a |
A、(-
| ||
B、(-
| ||
C、(
| ||
D、(
|
若向量
与
不共线,
•
≠0,且
=
-
,则向量
与
的夹角为( )
| a |
| b |
| a |
| b |
| c |
| a |
(
| ||||||
|
| a |
| c |
A、
| ||
B、
| ||
C、
| ||
| D、0 |
在平面直角坐标系xOy中,设不等式组
,所表示的平面区域为D,若D的边界是菱形,则ab=( )
|
A、-2
| ||
B、2
| ||
C、2
| ||
D、-2
|
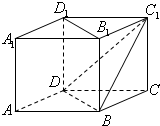
如图所示,在正方体ABCD-A1B1C1D1中,直线B1D1与平面BDC1的位置关系是( )

| A、平行 |
| B、垂直 |
| C、相交但不垂直 |
| D、直线B1D1在平面BDC1内 |