题目内容
13.设(1-x)(2x+1)5=a0+a1x+a2x2+…+a5x6,则a2等于30.分析 根据题意先求出(2x+1)5的通项,再计算展开式中含x2项的系数,从而求出a2的值.
解答 解:∵(1-x)(2x+1)5=a0+a1x+a2x2+…+a5x6,
而(2x+1)5=(1+2x)5展开式的通项为:
Tr+1=${C}_{5}^{r}$•2r•xr,
∴(1-x)(2x+1)5展开式中含x2的项为:
${C}_{5}^{2}$•22•x2-x•${C}_{5}^{1}$•2x=40x2-10x2=30x2,
∴a2=30.
故答案为:30.
点评 本题主要考查了二项展开式的通项公式在求解特定项中的应用问题,是基础题.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案
相关题目
3.执行如下图所示的程序框图,输出S的值为( )


| A. | 1007 | B. | 1008 | C. | 1009 | D. | 1010 |
8.复数$\frac{2i}{1-i}$在复平面内所对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
2.已知焦点为F的抛物线y2=2px(p>0)上有一点$A({m,2\sqrt{2}})$,以A为圆心,|AF|为半径的圆被y轴截得的弦长为$2\sqrt{7}$,则m=( )
| A. | $\frac{1}{3}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{\sqrt{6}}}{3}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |
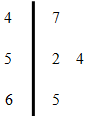 已知某路段最高限速60km/h,电子监控测得连续4辆汽车的速度用用茎叶图表示如图示,若从中任取2辆,则恰好有1辆汽车超速的概率为$\frac{1}{2}$.
已知某路段最高限速60km/h,电子监控测得连续4辆汽车的速度用用茎叶图表示如图示,若从中任取2辆,则恰好有1辆汽车超速的概率为$\frac{1}{2}$.