题目内容
已知椭圆C的中心为坐标原点O,一个长轴端点为(0,2),短轴端点和焦点所组成的四边形为正方形,直线l与y轴交于点P(0,m),与椭圆C交于相异两点A,B,且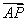 =2
=2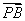 .
.
(1)求椭圆的方程;
(2)求m的取值范围.
解:(1)由题意知椭圆的焦点在y轴上,设椭圆方程为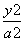 +
+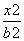 =1(a>b>0),
=1(a>b>0),
由题意知a=2,b=c,又a2=b2+c2,则b= ,所以椭圆的方程为
,所以椭圆的方程为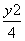 +
+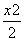 =1.
=1.
(2)设A(x1,y1),B(x2,y2),由题意知,直线l的斜率存在,设其方程为y=kx+m,与椭圆方程联立,
得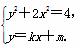
则(2+k2)x2+2mkx+m2-4=0,
Δ=(2mk)2-4(2+k2)(m2-4)>0.
由根与系数的关系知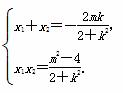
又由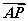 =2
=2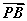 ,
,
即(-x1,m-y1)=2(x2,y2-m),
得-x1=2x2,故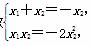
可得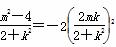
整理得(9m2-4)k2=8-2m2,又9m2-4=0时不符合题意,所以k2=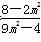 >0,解得
>0,解得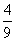 <m2<4,此时Δ>0,解不等式
<m2<4,此时Δ>0,解不等式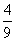 <m2<4得
<m2<4得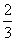 <m<2或-2<m<-
<m<2或-2<m<-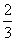 ,
,
所以m的取值范围为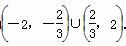 .
.

练习册系列答案
相关题目
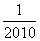 -
-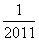 -
-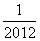 -
-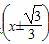 2+y2=
2+y2=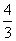 B.
B. 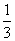
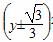 2=
2=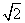 时,求直线l的方程.
时,求直线l的方程. =1表示焦点在x轴上的椭圆,则实数a的取值范围是________.
=1表示焦点在x轴上的椭圆,则实数a的取值范围是________.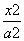 -
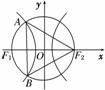
-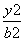 =1(a>0,b>0)的两个焦点,以坐标原点O为圆心,|OF1|为半径的圆与该双曲线左支的两个交点分别为A,B,且△F2AB是等边三角形,则双曲线的离心率为( )
=1(a>0,b>0)的两个焦点,以坐标原点O为圆心,|OF1|为半径的圆与该双曲线左支的两个交点分别为A,B,且△F2AB是等边三角形,则双曲线的离心率为( )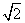 +1 B.
+1 B.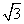 +1 C.
+1 C. 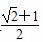 D.
D. 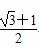
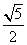 B.
B.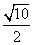
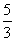 D.
D.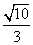
 中,
中, ,则
,则 的值是 。
的值是 。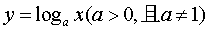 中,下列描述正确的是( )
中,下列描述正确的是( )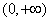 、值域是R ②图像必过点(1,0).
、值域是R ②图像必过点(1,0).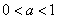 时,在
时,在 时,在
时,在