题目内容
已知双曲线x2-
=1的离心率为
,且抛物线y2=mx的焦点为F,点P(2,y0)(y0>0)在此抛物线上,M为线段PF的中点,则点M到该抛物线的准线的距离为( )
| y2 |
| 3 |
| m |
| 2 |
A、
| ||
| B、2 | ||
C、
| ||
| D、1 |
考点:抛物线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:依题意,可求得双曲线x2-
=1的离心率e=2,于是知m=4,从而可求抛物线y2=4x的焦点F(1,0),准线方程为x=-1,继而可得点M的横坐标为
,从而得到答案.
| y2 |
| 3 |
| 3 |
| 2 |
解答:
解:∵双曲线x2-
=1的离心率e=
=2=
,
∴m=4,
∴抛物线y2=mx=4x的焦点F(1,0),准线方程为x=-1;
又点P(2,y0)在此抛物线上,M为线段PF的中点,
∴点M的横坐标为:
=
,
∴点M到该抛物线的准线的距离d=
-(-1)=
,
故选:A.
| y2 |
| 3 |
| ||
| 1 |
| m |
| 2 |
∴m=4,
∴抛物线y2=mx=4x的焦点F(1,0),准线方程为x=-1;
又点P(2,y0)在此抛物线上,M为线段PF的中点,
∴点M的横坐标为:
| 1+2 |
| 2 |
| 3 |
| 2 |
∴点M到该抛物线的准线的距离d=
| 3 |
| 2 |
| 5 |
| 2 |
故选:A.
点评:本题考查抛物线的简单性质,考查双曲线的离心率,考查等价转化思想与运算求解能力,属于中档题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
动点P(m,n)到直线l:x=-5的距离为λ
,点P的轨迹为双曲线(且原点O为准线l对应的焦点),则λ的取值为( )
| m2+n2 |
| A、λ∈R | B、λ=1 |
| C、λ>1 | D、0<λ<1 |
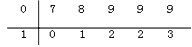 如图所示的茎叶图记录了一组数据,关于这组数据给出了如下四个结论:①众数是9;②平均数10;③中位数是9或10;④方差是3.4,其中正确命题的个数是( )
如图所示的茎叶图记录了一组数据,关于这组数据给出了如下四个结论:①众数是9;②平均数10;③中位数是9或10;④方差是3.4,其中正确命题的个数是( )