题目内容

已知函数f（x）=log2x，等比数列{an}的公比为2，若f（a2•a4…a10）=25，则a1=
 
．
考点：对数的运算性质
专题：函数的性质及应用,等差数列与等比数列
分析：根据等比数列的通项公式，以及对数的基本运算即可得到结论．
解答： 解：∵等比数列{an}的公比为2，
∴a2•a4…a10=（a6•）5=
a
5
1
225，
∵f（a2•a4…a10）=25，
∴f（=
a
5
1
225）=log2
a
5
1
225=25，
即=
a
5
1
225=225，
即a1=1，
故答案为：1
点评：本题主要考查等比数列应用，利用对数的基本运算法则是解决本题的关键．
练习册系列答案
相关题目
已知f（x）=axekx-1，g（x）=lnx+kx．
（Ⅰ）求g（x）的单调区间；
（Ⅱ）当k=1时，f（x）≥g（x）恒成立，求a的取值范围．
函数f（x）=3sin（2x-
π
3
）的图象为C，则如下结论中正确的序号是
 

①图象C关于直线x=
11
12
π对称； 
②函数f（x）在区间（-
π
12
，
5π
12
）内是增函数；
③图象C关于点（
2π
3
，0）对称； 
④当x=2kπ+
5
12
π，k∈z时f（x）取最大值．
若数列：12+22+32+42+…+n2=
n(n+1)(2n+1)
6
，则数列：1，2，2，3，3，3，4，4，4，4，…的前100项的和是
 
．
已知函数f（x）=
x2+2x+a，x＜0
lnx，x＞0
，其中a是实数．设A（x1，f（x1）），B（x2，f（x2））为该函数图象上的两点，且x1＜x2，若函数f（x）的图象在点A，B处的切线重合，则a的取值范围是
 
．
在（1+x）n的展开式中，若第三项和第六项的系数相等，则n=
 
．
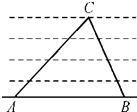如图，为了测定河的宽度，在一岸边选定两点A，B和对岸标记物C，测得∠CAB=30°，∠CBA=45°，AB=120m，则河的宽度为
 
m．
已知双曲线
x2
a2
-
y2
b2
=λ（a＞0，b＞0，λ≠0）的渐近线经过点（2，1），则双曲线的离心率e=
 
．
下列结论中：
①函数y=x（1-2x）（x＞0）有最大值
1
8

②函数y=2-3x-
4
x
（x＜0）有最大值2-4
3

③若a＞0，则(1+a)(1+
1
a
)≥4
正确的序号是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网