题目内容
18.已知A(-2,0),B(1,0)两点,动点P不在x轴上,且满足∠APO=∠BPO,其中O为原点,则P点的轨迹方程是( )| A. | (x+2)2+y2=4(y≠0) | B. | (x+1)2+y2=1(y≠0) | C. | (x-2)2+y2=4(y≠0) | D. | (x-1)2+y2=1(y≠0) |
分析 确定点P在∠APB的角平分线上,则利用PA:PB=AO:OB=2:1,即可得出结论.
解答 解:因为A(-2,0),B(1,0)两点,动点P不在x轴上,且满足∠APO=∠BPO,
所以点P在∠APB的角平分线上,则利用PA:PB=AO:OB=2:1,
设点P(x,y),则利用关系式可知$\sqrt{(x+2)^{2}+{y}^{2}}$=2$\sqrt{(x-1)^{2}+{y}^{2}}$,
化简可得(x-2)2+y2=4(y≠0).
故选:C.
点评 本题考查平分线的性质及直接法求轨迹方程,难度中等.

练习册系列答案
相关题目
7.已知直线l:kx-y+1-k=0与圆O:x2+y2=8交于P,Q两点,若圆O上有一个点E,使得OPEQ是平行四边形,则弦PQ的长为( )
| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 2$\sqrt{6}$ | D. | 2$\sqrt{10}$ |
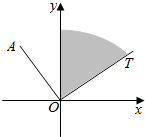 如图所示,在直角坐标系内,射线OT落在30°角的终边上,任作一条射线OA,则射线OA落在∠yOT内的概率为$\frac{1}{6}$.
如图所示,在直角坐标系内,射线OT落在30°角的终边上,任作一条射线OA,则射线OA落在∠yOT内的概率为$\frac{1}{6}$. 分别根据下列两个实际背景
分别根据下列两个实际背景