题目内容
已知函数f(x)=(x-a)lnx,a∈R.
(Ⅰ)若a=0,对于任意的x∈(0,1),求证:-
≤f(x)<0;
(Ⅱ)若函数f(x)在其定义域内不是单调函数,求实数a的取值范围.
(Ⅰ)若a=0,对于任意的x∈(0,1),求证:-
| 1 |
| e |
(Ⅱ)若函数f(x)在其定义域内不是单调函数,求实数a的取值范围.
考点:利用导数研究函数的单调性
专题:函数的性质及应用,导数的概念及应用,导数的综合应用
分析:(Ⅰ) 当a=0时,f(x)=xlnx,利用导数法,求出函数的最小值,进而根据x∈(0,1)时,lnx<0,进而f(x)<0,可得结论;
(Ⅱ)由f′(x)=
,设g(x)=xlnx+x-a.令g(x)=xlnx+x-a=0,即a=xlnx+x,设函数h(x)=xlnx+x.令h′(x)=lnx+2=0,则x=
.结合函数单调性与导数值的关系,可得a>-
即为所求.
(Ⅱ)由f′(x)=
| xlnx+x-a |
| x |
| 1 |
| e2 |
| 1 |
| e2 |
解答:
证明:(Ⅰ) 当a=0时,f(x)=xlnx,
∴f′(x)=lnx+1.
令f′(x)=lnx+1=0,解得x=
.
当x∈(0,
)时,f′(x)<0,所以函数f(x)在(0,
)是减函数;
当x∈(
,+∞)时,f′(x)>0,所以函数f(x)在(
,+∞)为增函数.
所以函数f(x)在x=
处取得最小值-
,
因为x∈(0,1)时,lnx<0,
所以对任意x∈(0,1),
都有f(x)<0,
即对任意x∈(0,1),
-
≤f(x)<0;…(6分)
(Ⅱ)函数f(x)的定义域为(0,+∞).
又f′(x)=
,
设g(x)=xlnx+x-a.
令g(x)=xlnx+x-a=0,即a=xlnx+x,
设函数h(x)=xlnx+x.
令h′(x)=lnx+2=0,则x=
.
当x∈(0,
)时,h′(x)<0,所以函数h(x)在(0,
)是减函数;
当x∈(
,+∞)时,h′(x)>0,所以函数h(x)在(
,+∞)为增函数.
所以函数h(x)在x=
处取得最小值-
,
则x∈(0,+∞)时,h(x)≥-
.
于是,当a≥-
时,直线y=a与函数h(x)=xlnx+x的图象有公共点,
即函数g(x)=xlnx+x-a至少有一个零点,也就是方程f′(x)=0至少有一个实数根.
当a=-
时,g(x)=xlnx+x-a有且只有一个零点,
所以f′(x)≥0恒成立,函数f(x)为单调增函数,不合题意,舍去.
即当a>-
时,函数f(x)不是单调增函数.
又因为f′(x)<0不恒成立,
所以a>-
为所求.…(13分)
∴f′(x)=lnx+1.
令f′(x)=lnx+1=0,解得x=
| 1 |
| e |
当x∈(0,
| 1 |
| e |
| 1 |
| e |
当x∈(
| 1 |
| e |
| 1 |
| e |
所以函数f(x)在x=
| 1 |
| e |
| 1 |
| e |
因为x∈(0,1)时,lnx<0,
所以对任意x∈(0,1),
都有f(x)<0,
即对任意x∈(0,1),
-
| 1 |
| e |
(Ⅱ)函数f(x)的定义域为(0,+∞).
又f′(x)=
| xlnx+x-a |
| x |
设g(x)=xlnx+x-a.
令g(x)=xlnx+x-a=0,即a=xlnx+x,
设函数h(x)=xlnx+x.
令h′(x)=lnx+2=0,则x=
| 1 |
| e2 |
当x∈(0,
| 1 |
| e2 |
| 1 |
| e2 |
当x∈(
| 1 |
| e2 |
| 1 |
| e2 |
所以函数h(x)在x=
| 1 |
| e2 |
| 1 |
| e2 |
则x∈(0,+∞)时,h(x)≥-
| 1 |
| e2 |
于是,当a≥-
| 1 |
| e2 |
即函数g(x)=xlnx+x-a至少有一个零点,也就是方程f′(x)=0至少有一个实数根.
当a=-
| 1 |
| e2 |
所以f′(x)≥0恒成立,函数f(x)为单调增函数,不合题意,舍去.
即当a>-
| 1 |
| e2 |
又因为f′(x)<0不恒成立,
所以a>-
| 1 |
| e2 |
点评:本题考查的知识点是对数函数的图象和性质,利用导数求函数的最值,利用导数求函数的单调性.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
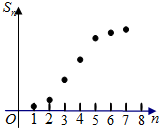 某工厂前n年的总产量Sn与n之间的关系如图所示.从目前记录的结果看,前m年的年平均产量最高.m值为( )
某工厂前n年的总产量Sn与n之间的关系如图所示.从目前记录的结果看,前m年的年平均产量最高.m值为( )| A、2 | B、4 | C、5 | D、8 |
设函数f(x)的零点为x1,g(x)=4x+2x-2的零点为x2,若|x1-x2|≤0.25,则f(x)可以是( )
| A、f(x)=(x-1)2 | ||
| B、f(x)=ex-1 | ||
C、f(x)=ln(x-
| ||
| D、f(x)=4x-1 |
已知奇函数f(x)当x>0时,f(x)=x(1-x),则当x<0时,f(x)的表达式是( )
| A、-x(1-x) |
| B、x(1+x) |
| C、-x(1+x) |
| D、x(1-x) |