题目内容
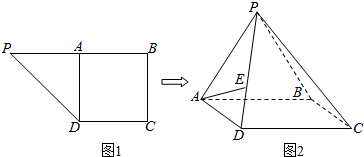
14. 如图,四边形ABCD是菱形,PD⊥平面ABCD,PD∥BE,AD=PD=2BE=2,∠DAB=60°,点F为PA的中点.
如图,四边形ABCD是菱形,PD⊥平面ABCD,PD∥BE,AD=PD=2BE=2,∠DAB=60°,点F为PA的中点.(Ⅰ)求证:EF∥平面ABCD;
(Ⅱ)求证:平面PAE⊥平面PAD;
(Ⅲ)求三棱锥P-ADE的体积.
分析 (Ⅰ)取AD中点G,连接FG,BG,则可证四边形BGFE为平行四边形.故EF∥BG,从而EF∥平面ABCD;
(II)由△ABD是等边三角形可得BG⊥AD,由PD⊥平面ABCD可得BG⊥PD,故BG⊥平面PAD,由EF∥BG可证EF⊥平面PAD,从而平面PAE⊥平面PAD;
(III)V棱锥P-ADE=V棱锥E-ADP=$\frac{1}{3}$S△PAD•EF.
解答  解:(Ⅰ)取AD中点G,连接FG,BG,∵点F为PA的中点,
解:(Ⅰ)取AD中点G,连接FG,BG,∵点F为PA的中点,
∴FG∥PD且$FG=\frac{1}{2}PD$.
∵BE∥PD,且$BE=\frac{1}{2}PD$,
∴BE∥FG,BE=FG,
∴四边形BGFE为平行四边形.
∴EF∥BG,又∵EF?平面ABCD,BG?平面ABCD,
∴EF∥平面ABCD.
(Ⅱ)连接BD.
∵四边形ABCD为菱形,∠DAB=60°,∴△ABD为等边三角形.
∵G为AD中点,∴BG⊥AD,
∵PD⊥平面ABCD,BG?平面ABCD,
∴PD⊥BG,又∵PD∩AD=D,AD?平面PAD,PD?平面PAD,
∴BG⊥平面PAD.
∵四边形BGFE为平行四边形,∴EF∥BG,
∴EF⊥平面PAD,又∵EF?平面PAE,
∴平面PAE⊥平面PAD.
(Ⅲ)∵△ABD为等边三角形,AD=2,∴BG=$\sqrt{3}$.
∵${S_{△PAD}}=\frac{1}{2}PD•AD=2$.$EF=BG=\sqrt{3}$,∴V棱锥P-ADE=V棱锥E-ADP=$\frac{1}{3}$S△PAD•EF=$\frac{2\sqrt{3}}{3}$.
点评 本题考查了线面平行的判定,面面垂直的判定,棱锥的体积计算,是中档题.

练习册系列答案
相关题目
5.直线y=kx-2交抛物线y2=8x于A、B两点,若AB中点横坐标为2,则|AB|为( )
| A. | $\sqrt{15}$ | B. | $2\sqrt{15}$ | C. | $\sqrt{42}$ | D. | $3\sqrt{15}$ |
2.椭圆$\frac{x^2}{3}+\frac{y^2}{5}=1$的焦距是( )
| A. | $2\sqrt{2}$ | B. | $4\sqrt{2}$ | C. | 2 | D. | $\sqrt{2}$ |
19.一个几何体的三视图如图所示,则该几何体的表面积为( )
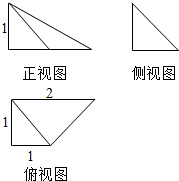

| A. | $\frac{3}{2}$ | B. | $\frac{{6+\sqrt{2}+\sqrt{6}}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{{3+\sqrt{2}+\sqrt{6}}}{2}$ |
6.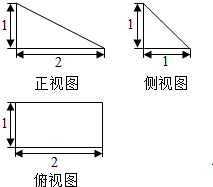 某几何体的正视图、侧(左)视图、俯视图如图所示,若该几何体各个顶点在同一个球面上,则该球体的表面积是( )
某几何体的正视图、侧(左)视图、俯视图如图所示,若该几何体各个顶点在同一个球面上,则该球体的表面积是( )
 某几何体的正视图、侧(左)视图、俯视图如图所示,若该几何体各个顶点在同一个球面上,则该球体的表面积是( )
某几何体的正视图、侧(左)视图、俯视图如图所示,若该几何体各个顶点在同一个球面上,则该球体的表面积是( )| A. | 6π | B. | 12π | C. | 24π | D. | 32π |
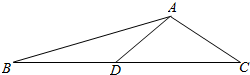 在△ABC中,∠BAD=30°,AB=4,AC=2,点D在BC上,且BC=2BD
在△ABC中,∠BAD=30°,AB=4,AC=2,点D在BC上,且BC=2BD