题目内容
19.一个几何体的三视图如图所示,则该几何体的表面积为( )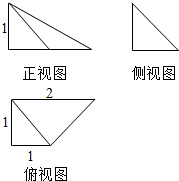
| A. | $\frac{3}{2}$ | B. | $\frac{{6+\sqrt{2}+\sqrt{6}}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{{3+\sqrt{2}+\sqrt{6}}}{2}$ |
分析 由三视图判断出几何体是四棱锥,且底面是直角梯形,依据三视图的数据,求出表面积
解答 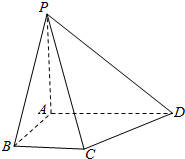 解:由三视图判断出几何体是四棱锥,且底面是直角梯形高为PA;
解:由三视图判断出几何体是四棱锥,且底面是直角梯形高为PA;
S△PAB=$\frac{1}{2}×$1×1=$\frac{1}{2}$,S△PBC=$\frac{1}{2}×1$×$\sqrt{2}$=$\frac{\sqrt{2}}{2}$,S△PAD=$\frac{1}{2}×2×1$=1,S梯形=$\frac{1}{2}×$(1+2)×1=$\frac{3}{2}$,
∵PA=1,AC=$\sqrt{2}$,PC=$\sqrt{3}$,CD=$\sqrt{2}$,PD=$\sqrt{5}$,∴Rt△PCD的面积=$\frac{1}{2}×\sqrt{2}×\sqrt{3}$=$\frac{\sqrt{6}}{2}$,
表面积为:$\frac{1}{2}+1+\frac{3}{2}$$+\frac{\sqrt{2}}{2}$$+\frac{\sqrt{6}}{2}$=$\frac{6+\sqrt{2}+\sqrt{6}}{2}$
故选;B
点评 本题考查了运用空间思维能力解决空间几何体的方法,运用三视图得出空间几何体的结构特征是解题的关键.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
7.已知点P是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)右支上一点,以P为圆心能作一圆恰好过双曲线的左顶点A和右焦点F,则该双曲线的离心率e的取值范围为( )
| A. | (1,2] | B. | (1,3] | C. | [2,+∞) | D. | [3,+∞) |
11.已知正三棱锥V-ABC的正视图、侧视图和俯视图如图所示,则该正三棱锥侧视图的面积是( )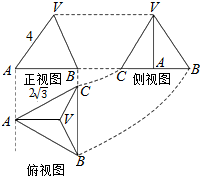

| A. | $\sqrt{39}$ | B. | 6$\sqrt{3}$ | C. | 8$\sqrt{3}$ | D. | 6 |
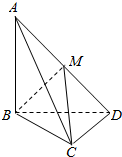 如图,三棱锥A-BCD中,AB=BD=CD=1,AD=BC=$\sqrt{2}$,AC=$\sqrt{3}$.
如图,三棱锥A-BCD中,AB=BD=CD=1,AD=BC=$\sqrt{2}$,AC=$\sqrt{3}$.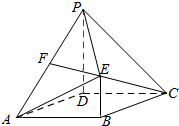 如图,四边形ABCD是菱形,PD⊥平面ABCD,PD∥BE,AD=PD=2BE=2,∠DAB=60°,点F为PA的中点.
如图,四边形ABCD是菱形,PD⊥平面ABCD,PD∥BE,AD=PD=2BE=2,∠DAB=60°,点F为PA的中点. 已知某几何体的三视图如图所示,(图中每一格为1个长度单位)则该几何体的全面积为4+4$\sqrt{5}$.
已知某几何体的三视图如图所示,(图中每一格为1个长度单位)则该几何体的全面积为4+4$\sqrt{5}$.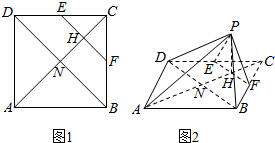 如图1,正方形ABCD的边长为$2\sqrt{2}$,E、F分别是DC和BC的中点,H是正方形的对角线AC与EF的交点,N是正方形两对角线的交点,现沿EF将△CEF折起到△PEF的位置,使得PH⊥AH,连结PA,PB,PD(如图2).
如图1,正方形ABCD的边长为$2\sqrt{2}$,E、F分别是DC和BC的中点,H是正方形的对角线AC与EF的交点,N是正方形两对角线的交点,现沿EF将△CEF折起到△PEF的位置,使得PH⊥AH,连结PA,PB,PD(如图2).