题目内容
14.曲线$\left\{\begin{array}{l}{x=sinθ}\\{y=cos2θ}\end{array}\right.$(θ参数)在y轴上的截距为( )| A. | 、$-\frac{1}{2}$ | B. | -1 | C. | $\frac{1}{2}$ | D. | 1 |
分析 利用倍角公式化为普通方程,令x=0,解得y即可得出在y轴上的截距.
解答 解:曲线$\left\{\begin{array}{l}{x=sinθ}\\{y=cos2θ}\end{array}\right.$(θ参数),可得:y=1-2sin2θ=1-2x2,
令x=0,解得y=1.
∴在y轴上的截距为1.
故选:D.
点评 本题考查了倍角公式、截距,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
18.为了解高中生对电视台某节目的态度,在某中学随机调查了110名学生,得到如下列联表:
由${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$算得${K^2}=\frac{{110×{{({40×30-20×20})}^2}}}{60×50×60×50}≈7.8$.
附表:
参照附表,得到的正确结论是( )
| 男 | 女 | 总计 | |
| 喜欢 | 40 | 20 | 60 |
| 不喜欢 | 20 | 30 | 50 |
| 总计 | 60 | 50 | 110 |
附表:
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
| A. | 在犯错误的概率不超过0.1%的前提下,认为“喜欢该节目与性别有关” | |
| B. | 在犯错误的概率不超过0.1%的前提下,认为“喜欢该节目与性别无关” | |
| C. | 有99%以上的把握认为“喜欢该节目与性别有关” | |
| D. | 有99%以上的把握认为“喜欢该节目与性别无关” |
2.若如图框图所给的程序运行结果为S=41,图中的判断框①中是i>a,则实数a的取值范围是( )
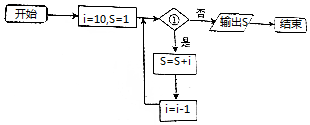

| A. | (5,6] | B. | [5,6) | C. | (6,7] | D. | [6,7) |
3.从1,2,3,4,5这五个数字中选出三个不相同数组成一个三位数,则奇数位上必须是奇数的三位数个数为( )
| A. | 12 | B. | 18 | C. | 24 | D. | 30 |