题目内容
16. 从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:
从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:| 质量指标值分组 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125) |
| 频数 | 6 | 26 | 38 | 22 | 8 |
(2)估计这种产品质量指标值的中位数、平均数及方差(同一组中的数据用该组区间的中点值作代表)(精确到0.01);
(3)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品80%”的规定?
分析 (1)由已知作出频率分布表,由此能作出作出这些数据的频率分布直方图.
(2)由频率分布直方图能求出质量指标值的样本中位数、平均数及方差.
(3)质量指标值不低于95的产品所占比例的估计值.由于该估计值小于0.8,故不能认为该企业生产的这种产品“质量指标值不低于95 的产品至少要占全部产品80%的规定.
解答 解:(1)由已知作出频率分布表为:
| 质量指标值分组 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125) |
| 频数 | 6 | 26 | 38 | 22 | 8 |
| 频率 | 0.06 | 0.26 | 0.38 | 0.22 | 0.08 |
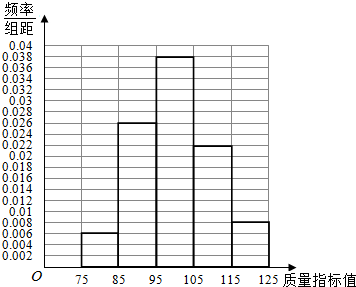
(2)质量指标值的样本平均数为:$\overline{x}$=80×0.06+90×0.26+100×0.38+110×0.22+120×0.08=100.
∵[75,95)内频率为:0.06+0.26=0.32,
∴中位数位于[95,105)内,
设中位数为x,则x=95+$\frac{0.5-0.26-0.06}{0.38}$≈99.7,
∴中位数为99.7.
S2=(-20)2×0.06+(-10)2×0.26+0×0.38+102×0.22+202×0.08=104
(3)质量指标值不低于95 的产品所占比例的估计值为 0.38+0.22+0.08=0.68.
由于该估计值小于0.8,
故不能认为该企业生产的这种产品“质量指标值不低于95 的产品至少要占全部产品80%的规定.
点评 本题考查频率分布直方图的作法,考查平均数、中位数、方差的求法,考查产品质量指标所占比重的估计值的计算与应用,是基础题.

练习册系列答案
相关题目
18.若y=f(x)是定义域在R上的函数,则y=f(x)为奇函数的一个充要条件为( )
| A. | f(0)=0 | B. | 对?x∈R,f(x)=0都成立 | ||
| C. | ?x0∈R,使得f(x0)+f(-x0)=0 | D. | 对?x∈R,f(x)+f(-x)=0都成立 |
7.如图给出了计算S=$\frac{1}{2}$+$\frac{1}{4}$+…+$\frac{1}{60}$的值的程序框图,其中 ①②分别是( )
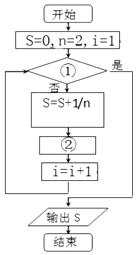

| A. | i<30,n=n+2 | B. | i>30,n=n+2 | C. | i<30,n=n+1 | D. | i>30,n=n+1 |
6.数列{an}满足${a_{n+1}}=\left\{\begin{array}{l}2{a_n},0≤{a_n}≤\frac{1}{2}\\ 2{a_n}-1,\frac{1}{2}≤{a_n}<1\end{array}\right.$,若${a_1}=\frac{6}{7}$,则a2017的值为( )
| A. | $\frac{6}{7}$ | B. | $\frac{5}{7}$ | C. | $\frac{3}{7}$ | D. | $\frac{1}{7}$ |
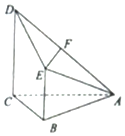 已知四棱锥A-BCDE中,侧面△ABC为等边三角形,BE=AB,CD=2AB,CD∥BE,且CD⊥平面ABC,F为棱AD的中点.
已知四棱锥A-BCDE中,侧面△ABC为等边三角形,BE=AB,CD=2AB,CD∥BE,且CD⊥平面ABC,F为棱AD的中点.