题目内容
| 2 |
| 1-x |
考点:其他不等式的解法
专题:不等式的解法及应用
分析:根据分式不等式的解法即可得到结论.
解答:
解:不等式
+a>0等价为
>0,
即(x-1)(ax-a-2)>0,
若a=0,则不等式等价为-2(x-1)>0,解得x<1,
若a>0,则不等式解得为a(x-1)(x-1-
)>0,即(x-1)(x-1-
)>0,
对应方程(x-1)(x-1-
)=0的根为x=1或x=1+
,
则1+
>1,则此时不等式的解为x>1+
或x<1,
若a<0,则不等式解得为a(x-1)(x-1-
)>0,即(x-1)(x-1-
)<0,
对应方程(x-1)(x-1-
)=0的根为x=1或x=1+
,
则1+
<1,则此时不等式的解为1<x<1+
,
故不等式的解集为当a=0,解集为(-∞,1),
当a>0时,解集为{x|x>1+
或x<1},
当a<0时,解集为{x|1<x<1+
}.
| 2 |
| 1-x |
| 2+a-ax |
| 1-x |
即(x-1)(ax-a-2)>0,
若a=0,则不等式等价为-2(x-1)>0,解得x<1,
若a>0,则不等式解得为a(x-1)(x-1-
| 2 |
| a |
| 2 |
| a |
对应方程(x-1)(x-1-
| 2 |
| a |
| 2 |
| a |
则1+
| 2 |
| a |
| 2 |
| a |
若a<0,则不等式解得为a(x-1)(x-1-
| 2 |
| a |
| 2 |
| a |
对应方程(x-1)(x-1-
| 2 |
| a |
| 2 |
| a |
则1+
| 2 |
| a |
| 2 |
| a |
故不等式的解集为当a=0,解集为(-∞,1),
当a>0时,解集为{x|x>1+
| 2 |
| a |
当a<0时,解集为{x|1<x<1+
| 2 |
| a |
点评:本题主要考查不等式的求解,要注意对a进行分类讨论.

练习册系列答案
相关题目
条件语句的一般形式如图所示,其中B表示的是( )


| A、条件 |
| B、条件语句 |
| C、满足条件时执行的内容 |
| D、不满足条件时执行的内容 |
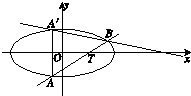 如图所示,已知椭圆C:
如图所示,已知椭圆C: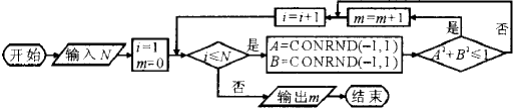

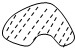 如图,边长为2的正方形中有一封闭曲线围成的阴影区域.在正方形中随机撒一粒豆子,它落在阴影区域内的概率为
如图,边长为2的正方形中有一封闭曲线围成的阴影区域.在正方形中随机撒一粒豆子,它落在阴影区域内的概率为