题目内容
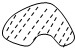如图，边长为2的正方形中有一封闭曲线围成的阴影区域．在正方形中随机撒一粒豆子，它落在阴影区域内的概率为| 3 |
| 4 |
考点：几何概型
专题：概率与统计
分析：本题考查的知识点是根据几何概型的意义进行模拟试验，计算不规则图形的面积，关键是要根据几何概型的计算公式，列出豆子落在阴影区域内的概率与阴影部分面积及正方形面积之间的关系．
解答：
解：正方形中随机撒一粒豆子，它落在阴影区域内的概率，
P=
=
，
又∵S正方形=4，
∴S阴影=3；
故答案为：3
P=
| S阴影 |
| S正方形 |
| 3 |
| 4 |
又∵S正方形=4，
∴S阴影=3；
故答案为：3
点评：本题考查了几何概型的运用；利用几何概型的意义进行模拟试验，估算不规则图形面积的大小，关键是要根据几何概型的计算公式，探究不规则图形面积与已知的规则图形的面积之间的关系，及它们与模拟试验产生的概率（或频数）之间的关系，并由此列出方程，解方程即可得到答案．
练习册系列答案
相关题目
已知两直线a1x+b1y+1=0和a2x+b2y+1=0的交点为P（2，3），求过两点A（a1，b1）、B（a2，b2）（a1≠a2）的直线方程（ ）
| A、3x+2y+1=0 |
| B、5x+y+1=0 |
| C、x+5y+1=0 |
| D、2x+3y+1=0 |
若a∈R，则“a2＞a”是“a＞1”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、既不充分也不必要条件 |
| D、充要条件 |