题目内容
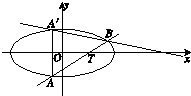 如图所示,已知椭圆C:
如图所示,已知椭圆C:| x2 |
| 4 |
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:设出A,B的坐标:A(x1,y1),B(x2,y2),A′(x1,-y1),设出直线AB的方程,y=k(x-1).联立椭圆的方程并消去y得到关于x的方程,根据韦达定理即可求x1+x2,x1x2,根据A′,B的坐标写出直线A′B的方程,并令y=0,便得到直线A′B与x轴交点的横坐标x=
,用x1,x2表示y1,y2并带入x即可求出x值,从而得到A′B经过x轴上的定点.
| y2x1+y1x2 |
| y1+y2 |
解答:
解:设A(x1,y1),B(x2,y2),则A′(x1,-y1);
由题意可知直线AB的斜率存在,设为k,直线方程为:y=k(x-1);
联立
,消去y得,(
+k2)x2-2k2x+k2-1=0;
∴x1+x2=
,x1x2=
;
直线A′B的方程为:y+y1=
(x-x1);
∴令y=0,x=
;
∵y1=k(x1-1),y2=k(x2-1);
∴y2+y1=k(x1+x2)-2k=
;
y2x1+y1x2=k(x2-1)x1+k(x1-1)x2=
;
∴x=
=4,即直线A′B经过x轴上的定点为(4,0).
故答案为:(4,0).
由题意可知直线AB的斜率存在,设为k,直线方程为:y=k(x-1);
联立
|
| 1 |
| 4 |
∴x1+x2=
| 2k2 | ||
|
| k2-1 | ||
|
直线A′B的方程为:y+y1=
| y2+y1 |
| x2-x1 |
∴令y=0,x=
| y2x1+y1x2 |
| y2+y1 |
∵y1=k(x1-1),y2=k(x2-1);
∴y2+y1=k(x1+x2)-2k=
-
| ||
|
y2x1+y1x2=k(x2-1)x1+k(x1-1)x2=
| -2k | ||
|
∴x=
| ||||||
|
故答案为:(4,0).
点评:考查关于x轴对称的点的坐标的关系,直线与椭圆的位置关系,直线的点斜式方程,以及韦达定理,求直线与x轴交点的方法:令y=0.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
用辗转相除法,计算56和264的最大公约数时,需要做的除法次数是( )
| A、3 | B、4 | C、6 | D、7 |
已知a>b>0,且|lga|=|lgb|,则函数f(x)=ax+x-b的零点落在区间( )
| A、(-2,-1) |
| B、(-1,0) |
| C、(0,1) |
| D、(1,2) |

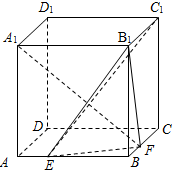 如图,在棱长为2的正方体ABCD-A1B1C1D1中,点E,F分别是棱AB,BC上的动点,且AE=BF.
如图,在棱长为2的正方体ABCD-A1B1C1D1中,点E,F分别是棱AB,BC上的动点,且AE=BF.