题目内容
在△ABC中,∠C=2∠A,cos∠A=
,
•
=
.求
(1)cos∠B的值;
(2)边AC的长.
| 3 |
| 4 |
| BA |
| BC |
| 27 |
| 2 |
(1)cos∠B的值;
(2)边AC的长.
考点:平面向量数量积的运算
专题:计算题,三角函数的求值,平面向量及应用
分析:(1))由∠C=2∠A,得到∠B=π-3∠A,再由诱导公式和二倍角公式及两角和的余弦公式,即可得到cos∠B的值;
(2)由cos∠A=
,得到sin∠A,再求得sinC,由正弦定理求出
,再由平面向量的数量积的定义,可得ac的值,解出a,c,再由余弦定理,即可得到b.
(2)由cos∠A=
| 3 |
| 4 |
| a |
| c |
解答:
解:(1)∵∠C=2∠A,
∴∠B=π-∠A-∠C=π-3∠A,
∴cos∠B=-cos3∠A=-cos(2∠A+∠A)
=-(cos2∠Acos∠A-sin2∠Asin∠A)
=-(2cos3∠A-cos∠A-2sin2∠Acos∠A)
=3cos∠A-4cos3∠A
=3×
-4×(
)3=
;
(2)由cos∠A=
,则sin∠A=
=
,
sinC=sin2∠A=2sin∠Acos∠A=2×
×
=
,
由正弦定理可得,
=
=
,
由
•
=
,得cacos∠B=
,
则ac=
×
=24,
即有a=4,c=6,
则由余弦定理得,b2=a2+c2-2accos∠B=16+36-2×4×6×
=25,
则b=5.
故边AC的长为5.
∴∠B=π-∠A-∠C=π-3∠A,
∴cos∠B=-cos3∠A=-cos(2∠A+∠A)
=-(cos2∠Acos∠A-sin2∠Asin∠A)
=-(2cos3∠A-cos∠A-2sin2∠Acos∠A)
=3cos∠A-4cos3∠A
=3×
| 3 |
| 4 |
| 3 |
| 4 |
| 9 |
| 16 |
(2)由cos∠A=
| 3 |
| 4 |
1-
|
| ||
| 4 |
sinC=sin2∠A=2sin∠Acos∠A=2×
| 3 |
| 4 |
| ||
| 4 |
3
| ||
| 8 |
由正弦定理可得,
| a |
| c |
| sin∠A |
| sin∠C |
| 2 |
| 3 |
由
| BA |
| BC |
| 27 |
| 2 |
| 27 |
| 2 |
则ac=
| 27 |
| 2 |
| 16 |
| 9 |
即有a=4,c=6,
则由余弦定理得,b2=a2+c2-2accos∠B=16+36-2×4×6×
| 9 |
| 16 |
则b=5.
故边AC的长为5.
点评:本题考查三角函数的化简和求值,考查余弦定理和正弦定理及运用,平面向量的数量积的运用,考查三角函数的恒等变换的运算能力,属于中档题.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
函数f(x)=
x+log2x的零点所在区间为( )
| π |
| 2 |
A、[0,
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
设a∈R,若函数f(x)=ex-ax,x∈R有大于零的极值点,则( )
| A、a<1 | ||
| B、a>1 | ||
C、a<
| ||
D、a>
|
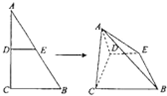 直角三角形ABC中,∠ACB=90°,AB=2BC=2,D、E分别为AC、AB边的中点.将△ADE沿DF折起,使△ADE沿DE折起,使△ADC为等边三角形,如图所示.
直角三角形ABC中,∠ACB=90°,AB=2BC=2,D、E分别为AC、AB边的中点.将△ADE沿DF折起,使△ADE沿DE折起,使△ADC为等边三角形,如图所示.