题目内容
9.已知函数$f(x)=\left\{\begin{array}{l}cos\frac{πx}{2},-1≤x≤1\\{x^2}-1,|x|>1\end{array}\right.$,则关于x的方程f2(x)-3f(x)+2=0的实根的个数是 ( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 先解出f(x)=1或f(x)=2,再结合函数图象,得到方程f(x)=1或2分别有3个根和2个根,故共有5个根,即为结果.
解答  解:根据函数f(x)的解析式,作出f(x)的图象,如右图,
解:根据函数f(x)的解析式,作出f(x)的图象,如右图,
再由方程f2(x)-3f(x)+2=0,
解得,f(x)=1或f(x)=2,分类讨论如下:
①当f(x)=1时,由图可知,该方程有3三解,
②当f(x)=2时,由图可知,该方程有2三解,
综合知,原方程f2(x)-3f(x)+2=0共有5解,
故答案为:D.
点评 本题主要考查了根的存在及根的个数判断,涉及三角函数和二次函数的图象和性质,体现了数形结合的解题思想,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.为了宣传2015年10月在贵阳举行的“世界众筹大会”,“世界众筹大会”筹委会举办了“大众创业、万众创新”知识有奖问答活动,随机对市民15~65岁的人群抽样n人,回答问题统计结果如图所示:
(1)分别求出a,x的值;
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,“世界众筹大会”筹委会决定给所抽取的6人颁发幸运奖,各组抽取的人数分别是多少?
(3)请根据频率分布直方图,估计样本数据的众数和中位数.
| 组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的频率 | 频率分布直方图 |
| 第1组 | [15,25) | 5 | 0.5 | 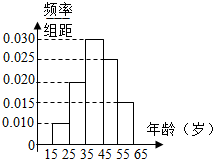 |
| 第2组 | [25,35) | a | 0.9 | |
| 第3组 | [35,45) | 27 | x | |
| 第4组 | [45,55) | 9 | 0.36 | |
| 第5组 | [55,65] | 3 | 0.2 |
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,“世界众筹大会”筹委会决定给所抽取的6人颁发幸运奖,各组抽取的人数分别是多少?
(3)请根据频率分布直方图,估计样本数据的众数和中位数.