题目内容
12.已知f(x)为奇函数,f(x)=$\left\{\begin{array}{l}{lo{g}_{\frac{1}{2}}(x+1),x∈[0,1)}\\{1-|x-3|,x∈[1,+∞)}\end{array}\right.$,方程f(x)=a(0<a<1)的所有实数根之和为( )| A. | 1-2a | B. | 2a-1 | C. | ($\frac{1}{2}$)a-1 | D. | 1-($\frac{1}{2}$)a |
分析 利用奇函数得出f(x)$\left\{\begin{array}{l}{-lo{g}_{\frac{1}{2}}(1-x),x∈(-1,0)}\\{-1+|x+3|,x∈(-∞,-1]}\end{array}\right.$,并画出图象,根据对称性得出x1+x2+x3+x4+x5=x3,再求出x3=1-2a即可.
解答 解:∵f(x)=$\left\{\begin{array}{l}{lo{g}_{\frac{1}{2}}(x+1),x∈[0,1)}\\{1-|x-3|,x∈[1,+∞)}\end{array}\right.$,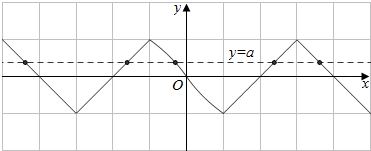
且f(x)为奇函数,
∴当x∈(-∞,0)时,
f(x)=$\left\{\begin{array}{l}{-lo{g}_{\frac{1}{2}}(1-x),x∈(-1,0)}\\{-1+|x+3|,x∈(-∞,-1]}\end{array}\right.$,
当a∈(0,1),方程f(x)=a有5个根,(如图)
从小到到依次设为:x1,x2,x3,x4,x5,
显然,x1与x2关于x=-3轴对称,x4,x5关于x=3对称,
即x1+x2=-6,x4+x5=6,
因此,所有实根之和为:x1+x2+x3+x4+x5=x3,
而x3∈(-1,0),故令-$lo{g}_{\frac{1}{2}}(1-x)$=a,
解得x3=1-2a,即x1+x2+x3+x4+x5=1-2a,
故答案为:A.
点评 本题主要函数的图象与性质,涉及函数的奇偶性和图象变换,并运用图象的对称性处理数量关系,体现了数形结合的解题思想,属于中档题.

练习册系列答案
相关题目
1.为了宣传2015年10月在贵阳举行的“世界众筹大会”,“世界众筹大会”筹委会举办了“大众创业、万众创新”知识有奖问答活动,随机对市民15~65岁的人群抽样n人,回答问题统计结果如图所示:
(1)分别求出a,x的值;
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,“世界众筹大会”筹委会决定给所抽取的6人颁发幸运奖,各组抽取的人数分别是多少?
(3)请根据频率分布直方图,估计样本数据的众数和中位数.
| 组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的频率 | 频率分布直方图 |
| 第1组 | [15,25) | 5 | 0.5 | 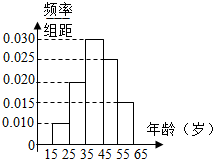 |
| 第2组 | [25,35) | a | 0.9 | |
| 第3组 | [35,45) | 27 | x | |
| 第4组 | [45,55) | 9 | 0.36 | |
| 第5组 | [55,65] | 3 | 0.2 |
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,“世界众筹大会”筹委会决定给所抽取的6人颁发幸运奖,各组抽取的人数分别是多少?
(3)请根据频率分布直方图,估计样本数据的众数和中位数.