题目内容
已知关于x的方程x2-2(a-3)x+9-b2=0,其中a,b都可以从集合{1,2,3,4,5,6}中任意选取,则已知
方程两根异号的概率为( )
方程两根异号的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:古典概型及其概率计算公式
专题:概率与统计
分析:关于x的方程x2-2(a-3)x+9-b2=0的两根异号,即△>0,9-b2<0,求出满足条件的(a,b)的数量,所有的(a,b)共有6×6个,二者的比值即是x2-2(a-3)x+9-b2=0的两根异号的概率.
解答:
解:∵x2-2(a-3)x+9-b2=0的两根异号,
∴△>0,9-b2<0,
∴4(a-3)2-4(9-b2)>0,9-b2<0,
∴b>3或b<-3(舍去)
∴b=4,5,6
所有的(a,b)共有6×6=36个,而满足b>3的(a,b)共有6×3,共有18个,
所以关于x的方程x2-2(a-3)x+9-b2=0的两根异号的概率是:
=
.
故选:B.
∴△>0,9-b2<0,
∴4(a-3)2-4(9-b2)>0,9-b2<0,
∴b>3或b<-3(舍去)
∴b=4,5,6
所有的(a,b)共有6×6=36个,而满足b>3的(a,b)共有6×3,共有18个,
所以关于x的方程x2-2(a-3)x+9-b2=0的两根异号的概率是:
| 18 |
| 36 |
| 1 |
| 2 |
故选:B.
点评:本题主要考查了概率的运算,考查了学生的分析推理能力,解答此题的关键是要弄清楚两点:①符合条件的情况数目;②全部情况的总数;二者的比值就是其发生的概率的大小.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
f(x)=
则f[f(
)]=( )
|
| 1 |
| 4 |
| A、9 | ||
B、
| ||
| C、1 | ||
| D、3 |
将函数y=2sinxsin(
+x)的图象向右平移φ(φ>0)个单位长度,使平移后的图象仍过点(
,
),则φ的最小值为( )
| π |
| 2 |
| π |
| 3 |
| ||
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
不等式2x-y-6<0表示的平面区域在直线2x-y-6=0的( )
| A、左上方 | B、右上方 |
| C、左下方 | D、右下方 |
若a>b,c∈R,则下列关系一定成立的是( )
| A、ac2>bc2 | ||||
| B、ac>bc | ||||
| C、a+c>b+c | ||||
D、
|
若函数f(x)=lnx+2x2-ax存在与直线2x-y=0平行的切线,则实数a取值范围是( )
| A、(-∞,-6] |
| B、(-∞,-6]∪[2,+∞) |
| C、[2,+∞) |
| D、(-∞,-6)∪(2,+∞) |
已知集合A={x|
≥0},B={x|y=log2(x+2)},则A∩B=( )
| x-1 |
| x+1 |
| A、(-2,-1) |
| B、(-2,-1)∪[1,+∞) |
| C、[1,+∞) |
| D、(-2,-1)∪(-1,+∞) |
已知函数f(x)=
(a∈R),则下列结论正确的是( )
|
| A、?a∈R,f(x)在R上单调递减 |
| B、?A∈R,f(x)的最小值为f(a) |
| C、?a∈R,f(x)有极大值和极小值 |
| D、?a∈R,f(x)有唯一零点 |
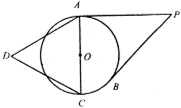 如图,半径为1的圆O外有一动点P,过P作圆O的切线PA,PB切于点A,B,以直径AC为一边作正三角形△ADC,则
如图,半径为1的圆O外有一动点P,过P作圆O的切线PA,PB切于点A,B,以直径AC为一边作正三角形△ADC,则