题目内容
双曲线
-y2=1的焦点到渐近线的距离为（ ）
| x2 |
| 4 |
| A、2 | ||
B、
| ||
| C、1 | ||
| D、3 |
考点：双曲线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：分别求出双曲线的焦点坐标和渐近线方程，利用点到直线的距离公式，能求出结果．
解答：
解：双曲线
-y2=1中，
焦点坐标为（±
，0），
渐近线方程为：y=±
x，
∴双曲线
-y2=1的焦点到渐近线的距离：
d=
=1．
故选：C．
| x2 |
| 4 |
焦点坐标为（±
| 5 |
渐近线方程为：y=±
| 1 |
| 2 |
∴双曲线
| x2 |
| 4 |
d=
|±
| ||
|
故选：C．
点评：本题考查双曲线的焦点到渐近线的距离的求法，是基础题，解题时要熟练掌握双曲线的简单性质．
练习册系列答案
相关题目
定义域为R的函数f（x）满足f（x+2）=2f（x），当x∈[0，2]时，f(x)=
，若x∈[-2，0]时，f(x)≥
-
恒成立，则实数t的取值范围是（ ）
|
| t |
| 2 |
| 1 |
| t |
| A、[-2，0）∪（0，1） |
| B、[-2，0）∪[1，+∞） |
| C、[-2，1] |
| D、（-∞，-2]∪（0，1] |
若对于任意的正数x，不等式3x（x2-2a）＞1恒成立，则a的取值范围是（ ）
| A、（-∞，+∞） | ||
| B、（-2，+∞） | ||
C、（
| ||
D、（-∞，-
|
阅读如图所示的程序框图，则该算法的功能是（ ）
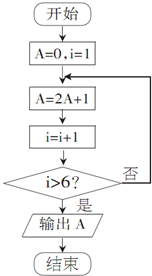
| A、计算数列{2n-1}前5项的和 |
| B、计算数列{2n-1}前6项的和 |
| C、计算数列{2n-1}前5项的和 |
| D、计算数列{2n-1}前6项的和 |
已知A，B，C是单位圆O上任意的不同三点，若
=2
+x
，则正实数x的取值范围为（ ）
| OA |
| OB |
| OC |
| A、（0，2] |
| B、[1，3] |
| C、[2，4] |
| D、[3，5] |
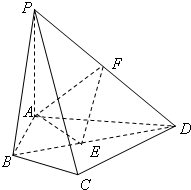如图，四棱锥P-ABCD中，PA⊥面ABCD，E、F分别为BD、PD的中点，EA=EB=AB=1，PA=2．