题目内容
16.某商家开展迎新春促销抽奖活动,小张、小李两人相约同一天上午去参加抽奖活动.(1)若抽奖规则是从一个装有3个红球和4个白球的袋中又放回地抽取2个球,当两球同色时则中奖,求中奖的概率;
(2)若小张计划在10:00~10:40之间赶到,小李计划在10:20~11:00之间赶到,求小张比小李提前到达的概率.
分析 (1)根据古典概型的概率公式进行计算即可.
(2)根据几何概型的概率公式求出对应事件对应区域的面积进行计算即可.
解答 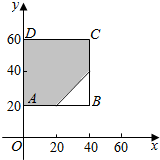 解:(1)从袋中7个球中的摸出2个,试验的结果共有7×7=49(种)…(1分)
解:(1)从袋中7个球中的摸出2个,试验的结果共有7×7=49(种)…(1分)
中奖的情况分为两种:
(i)2个球都是红色,包含的基本事件数为4×4=16;
(ii)2个球都是白色,包含的基本事件数为3×3=9. …(3分)
所以,中奖这个事件包含的基本事件数为16+9=25.
因此,中奖概率为$\frac{25}{49}$. …(5分)
(2)设小张和小李到达的时间分别为10点到11点之间的x,y分钟.
用(x,y)表示每次试验的结果,
则所有可能结果为Ω={(x,y)|0≤x≤4或0≤y≤60}; …(7分)
记小张比小李提前到达为事件A,则事件A的可能结果为
A={(x,y)|x<y,0≤x≤4或0≤y≤60};. …(9分)
如图所示,试验全部结果构成区域Ω为正方形ABCD.而事件A所构成区域是正方形内的阴影部分.
根据几何概型公式,得到P(A)=$\frac{{S}_{阴影}}{{S}_{正方形}}$=$\frac{4{0}^{2}-\frac{1}{2}×2{0}^{2}}{4{0}^{2}}$=$\frac{7}{8}$.
所以,小张比小李提前到达的概率为$\frac{7}{8}$. …(12分)
点评 本题主要考查古典概型和几何概型的概率的计算,根据对应分别求出对应区域的面积是解决本题的关键.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
6.一个几何体的顶点都在球面上,这个几何体的三视图如图所示,该球的表面积是( )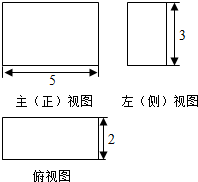

| A. | 19π | B. | 38π | C. | 48π | D. | $\frac{{19\sqrt{38}}}{3}π$ |
7.已知m,n是两条不同的直线,α,β是两个不同的平面,下列命题中正确的是( )
| A. | 若m?α,n?α,m∥β,n∥β,则α∥β | B. | 若m?α,m∥β,α∩β=n,则m∥n | ||
| C. | 若α∥β,m∥α,则m∥β | D. | 若m⊥n,n⊥β,β⊥α,则m⊥α |
11.一个圆内有一个内接等边三角形,一动点在圆内运动,则此点落在等边三角形内部的概率为( )
| A. | $\frac{3}{π}$ | B. | $\frac{{3\sqrt{3}}}{4π}$ | C. | $\frac{{\sqrt{3}}}{4π}$ | D. | $\frac{{2\sqrt{3}}}{3π}$ |
5.同时抛掷两枚骰子,向上点数之和为5的概率是( )
| A. | $\frac{1}{9}$ | B. | $\frac{2}{21}$ | C. | $\frac{1}{18}$ | D. | $\frac{1}{6}$ |
6.函数f(x)=x3的图象经过( )
| A. | 第一、三象限 | B. | 第二、三象限 | C. | 第一、二象限 | D. | 第一、四象限 |
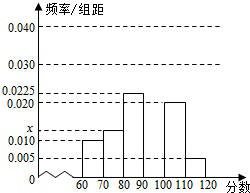 为了调查某校2000名高中生的体能情况,从中随机选取m名学生进行体能测试,将得到的成绩分成[60,70),[70,80),…,[110,120]六个组,并作出如下频率分布直方图,已知第四组的频数为12,图中从左到右的第一、二个矩形的面积比为4:5.规定:成绩在[60,70)、[70,90)、[90,110)、[110,120)的分别记为“不合格”、“合格”、“良好”,“优秀”,根据图中的信息,回答下列问题.
为了调查某校2000名高中生的体能情况,从中随机选取m名学生进行体能测试,将得到的成绩分成[60,70),[70,80),…,[110,120]六个组,并作出如下频率分布直方图,已知第四组的频数为12,图中从左到右的第一、二个矩形的面积比为4:5.规定:成绩在[60,70)、[70,90)、[90,110)、[110,120)的分别记为“不合格”、“合格”、“良好”,“优秀”,根据图中的信息,回答下列问题.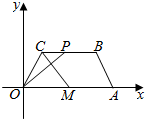 在平面直角坐标系xOy中,已知四边形OABC是等腰梯形,OA∥BC,$A(6,0),C(1,\sqrt{3})$,点M满足$\overrightarrow{OM}=\frac{1}{2}\overrightarrow{OA}$,点P在线段BC上运动(包括端点),如图.
在平面直角坐标系xOy中,已知四边形OABC是等腰梯形,OA∥BC,$A(6,0),C(1,\sqrt{3})$,点M满足$\overrightarrow{OM}=\frac{1}{2}\overrightarrow{OA}$,点P在线段BC上运动(包括端点),如图.