题目内容
7.从1,2,3,4,5,6,7中任取两个不同的数,事件A为“取到的两个数的和为偶数”,事件B为“取到的两个数均为奇数”则P(B|A)=( )| A. | $\frac{4}{7}$ | B. | $\frac{3}{7}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{2}$ |
分析 用列举法求出事件A为“取到的两个数的和为偶数”,事件B为“取到的两个数均为奇数”所包含的基本事件的个数,求P(A),P(AB),根据条件概率公式,即可得到结论.
解答 解:事件A=“取到的两个数之和为偶数”所包含的基本事件有:(1,3)、(1,5)、(1,7),(3,5)、(3,7),(5,7),(2,4),(2,6),(4,6)
∴P(A)=$\frac{9}{{C}_{7}^{2}}$=$\frac{3}{7}$,
事件B=“取到的两个数均为奇数”所包含的基本事件有(1,3),(1,5),(1,7),(3,5),(3,7),(5,7),
∴P(AB)=$\frac{6}{{C}_{7}^{2}}$=$\frac{2}{7}$
∴P(B|A)=$\frac{P(AB)}{P(A)}$=$\frac{2}{3}$.
故选C.
点评 本题考查条件概率的计算公式,同时考查学生对基础知识的记忆、理解和熟练程度.属于中档题.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
18.已知函数f(x)=$\frac{1}{3}$x${\;}^{3}-\frac{1}{2}m{x}^{2}+4x-3$在区间[1,2]上是增函数,则实数m的取值范围为( )
| A. | 4≤m≤5 | B. | 2≤m≤4 | C. | m≤2 | D. | m≤4 |
2.定义在R上的函数f(x)满足f'(x)-f(x)=x•ex,且$f(0)=\frac{1}{2}$,则$\frac{{x•{e^x}}}{f(x)}$的最大值为( )
| A. | 1 | B. | -$\frac{1}{2}$ | C. | -1 | D. | 0 |
17.已知集合A={1,2,3},B={0,1,2,4},则A∩B=( )
| A. | {0,1,2,3,4} | B. | {0,4} | C. | {1,2} | D. | {3} |
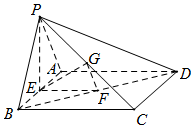 如图,在四棱锥P-ABCD中,底面ABCD是矩形,E,F,G分别是AB,BD,PC的中点,PE⊥底面ABCD.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,E,F,G分别是AB,BD,PC的中点,PE⊥底面ABCD.