题目内容
如图为函数y=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜| π |
| 2 |
（1）确定它的解析式；
（2）写出它的对称轴方程及对称中心．
考点：由y=Asin（ωx+φ）的部分图象确定其解析式
专题：三角函数的求值,三角函数的图像与性质
分析：（1）由图象可得A，从而解得ω，由函数的图象经过（
，0），可得φ，从而可求函数的解析式y=2sin（2x+
）；
（2）由2x+
=kπ+
，k∈Z可解得它的对称轴方程．由2x+
=kπ，k∈Z可解得它的对称中心．
| π |
| 10 |
| π |
| 5 |
（2）由2x+
| π |
| 5 |
| π |
| 2 |
| π |
| 5 |
解答：
解：（1）由图象可知：A=3…（3分）
T=2×（
+
）=π，
∴ω=2…..（6分）
函数的图象经过（
，0），
所以0=2sin[2×
+φ]，
∵φ+
=kπ，|φ|＜
，
∴φ=
．…（9分）
∴函数的解析式y=2sin（2x+
）…．（10分）
（2）由2x+
=kπ+
，k∈Z可解得它的对称轴方程为：x=
kπ+
，k∈Z
由2x+
=kπ，k∈Z可解得它的对称中心为：（
kπ-
，0），k∈Z…（12分）
T=2×（
| π |
| 10 |
| 2π |
| 5 |
∴ω=2…..（6分）
函数的图象经过（
| π |
| 10 |
所以0=2sin[2×
| π |
| 10 |
∵φ+
| π |
| 5 |
| π |
| 2 |
∴φ=
| π |
| 5 |
∴函数的解析式y=2sin（2x+
| π |
| 5 |
（2）由2x+
| π |
| 5 |
| π |
| 2 |
| 1 |
| 2 |
| 3π |
| 20 |
由2x+
| π |
| 5 |
| 1 |
| 2 |
| π |
| 10 |
点评：本题考查函数的解析式的求法，三角函数的图象和性质的应用，考查学生的视图用图能力，属于中档题．
练习册系列答案
相关题目
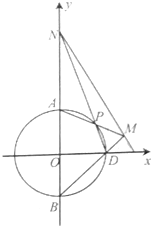如图所示，已知圆C：x2+y2=r2（r＞0）上点