题目内容
计算下列各式:
(1)(2
)
-(-9.6)0-(3
) -
+(1.5)-2;
(2)log3
+lg25+lg4+7log72
(3)求函数y=log2(x2-2x+3)的值域,并写出其单调区间.
(1)(2
| 1 |
| 4 |
| 1 |
| 2 |
| 3 |
| 8 |
| 2 |
| 3 |
(2)log3
| |||
| 3 |
(3)求函数y=log2(x2-2x+3)的值域,并写出其单调区间.
考点:对数的运算性质,复合函数的单调性,有理数指数幂的化简求值
专题:函数的性质及应用
分析:(1)根据指数的运算性质,代入可得答案;
(2)根据对数的运算性质,代入可得答案;
(3)利用换元法,结合二次函数的图象和性质及对数函数的图象和性质,可得函数的值域;进而根据复合函数单调性“同增异减”的原则,可得函数的单调区间.
(2)根据对数的运算性质,代入可得答案;
(3)利用换元法,结合二次函数的图象和性质及对数函数的图象和性质,可得函数的值域;进而根据复合函数单调性“同增异减”的原则,可得函数的单调区间.
解答:
解:(1)(2
)
-(-9.6)0-(3
) -
+(1.5)-2
=(
)
-1-[(
)3] -
+(
)-2
=
-1-(
)-2+(
)-2
=
;
(2)log3
+lg25+lg4+7log72
=log3
+lg(25×4)+2
=log33-
+lg100+2
=-
+4
=
;
(3)令t=x2-2x+3,则t≥2
函数y=log2(x2-2x+3)=log2t≥1,
故函数y=log2(x2-2x+3)的值域为[1,+∞),
又∵t=x2-2x+3在(-∞,1]上为减函数,在[1,+∞)上为增函数,
y=log2t为增函数,
故函数y=log2(x2-2x+3)的单调递增区间为[1,+∞),单调递减区间为(-∞,1].
| 1 |
| 4 |
| 1 |
| 2 |
| 3 |
| 8 |
| 2 |
| 3 |
=(
| 9 |
| 4 |
| 1 |
| 2 |
| 3 |
| 2 |
| 2 |
| 3 |
| 3 |
| 2 |
=
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
=
| 1 |
| 2 |
(2)log3
| |||
| 3 |
=log3
3
| ||
| 3 |
=log33-
| 1 |
| 4 |
=-
| 1 |
| 4 |
=
| 15 |
| 4 |
(3)令t=x2-2x+3,则t≥2
函数y=log2(x2-2x+3)=log2t≥1,
故函数y=log2(x2-2x+3)的值域为[1,+∞),
又∵t=x2-2x+3在(-∞,1]上为减函数,在[1,+∞)上为增函数,
y=log2t为增函数,
故函数y=log2(x2-2x+3)的单调递增区间为[1,+∞),单调递减区间为(-∞,1].
点评:本题考查的知识点是指数的运算性质,对数的运算性质,复合函数单调性,难度中档.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
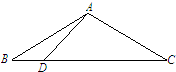 如图,△ABC中,AB=AC=2,BC=2
如图,△ABC中,AB=AC=2,BC=2