题目内容
 某单位设计一个展览沙盘,现欲在沙盘平面内,布设一个对角线在l上的四边形电气线路,如图所示.为充分利用现有材料,边BC,CD用一根5米长的材料弯折而成,边BA,AD用一根9米长的材料弯折而成,要求∠A和∠C互补,且AB=BC.记AB=x米,四边形ABCD面积为S,则S的最大值为( )
某单位设计一个展览沙盘,现欲在沙盘平面内,布设一个对角线在l上的四边形电气线路,如图所示.为充分利用现有材料,边BC,CD用一根5米长的材料弯折而成,边BA,AD用一根9米长的材料弯折而成,要求∠A和∠C互补,且AB=BC.记AB=x米,四边形ABCD面积为S,则S的最大值为( )| A、6 | ||
B、6
| ||
| C、8 | ||
D、8
|
考点:解三角形的实际应用
专题:综合题,导数的综合应用,解三角形
分析:在△ABD与△CBD中,分别利用余弦定理,即可确定cosA=
及x的取值范围;四边形ABCD的面积S=
(AB•AD+CB•CD)sinA=
,构建函数g(x)=(x2-4)( x2-14x+49),x∈(2,5),求导函数,即可求得四边形ABCD面积的最大值.
| 2 |
| x |
| 1 |
| 2 |
| (x2-4)(x2-14x+49) |
解答:
解:AB=x米,则BC=x米,CD=5-x米,AD=9-x米,则有5-x>0,即x<5.
在△ABD中,由余弦定理得BD2=AB2+AD2-2AB•AD•cosA.
同理,在△CBD中,BD2=CB2+CD2-2CB•CD•cosC.
因为∠A和∠C互补,所以AB2+AD2-2AB•AD•cosA=CB2+CD2-2CB•CD•cosC=CB2+CD2+2CB•CD•cosA.
即x2+(9-x)2-2 x(9-x)cosA=x2+(5-x)2+2 x(5-x)cosA.
解得cosA=
.
由余弦的定义,有
<1,则x>2,故x∈(2,5).
四边形ABCD的面积S=
(AB•AD+CB•CD)sinA=
[x(5-x)+x(9-x)]
=
.
记g(x)=(x2-4)(x2-14x+49),x∈(2,5).
由g′(x)=2x(x2-14x+49)+(x2-4)(2 x-14)=2(x-7)(2 x2-7 x-4)=0,
∴x=4或x=7或x=-
.
∵x∈(2,5),∴x=4.
∴函数g(x)在区间(2,4)内单调递增,在区间(4,5)内单调递减.
因此g(x)的最大值为g(4)=12×9=108.
∴S的最大值为6
.
故选:B.
在△ABD中,由余弦定理得BD2=AB2+AD2-2AB•AD•cosA.
同理,在△CBD中,BD2=CB2+CD2-2CB•CD•cosC.
因为∠A和∠C互补,所以AB2+AD2-2AB•AD•cosA=CB2+CD2-2CB•CD•cosC=CB2+CD2+2CB•CD•cosA.
即x2+(9-x)2-2 x(9-x)cosA=x2+(5-x)2+2 x(5-x)cosA.
解得cosA=
| 2 |
| x |
由余弦的定义,有
| 2 |
| x |
四边形ABCD的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1-cos2A |
| (x2-4)(x2-14x+49) |
记g(x)=(x2-4)(x2-14x+49),x∈(2,5).
由g′(x)=2x(x2-14x+49)+(x2-4)(2 x-14)=2(x-7)(2 x2-7 x-4)=0,
∴x=4或x=7或x=-
| 1 |
| 2 |
∵x∈(2,5),∴x=4.
∴函数g(x)在区间(2,4)内单调递增,在区间(4,5)内单调递减.
因此g(x)的最大值为g(4)=12×9=108.
∴S的最大值为6
| 3 |
故选:B.
点评:本题考查函数解析式,考查余弦定理的运用,考查四边形面积的计算,考查利用导数求函数的最值,正确表示四边形的面积是关键.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
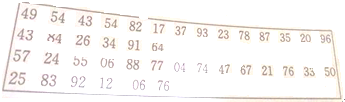 福利彩票“双色球”中,红球号码有编号为01,02,…,33的33个个体组成,某彩民利用下面的随机数表选取6组数作为6个红球的编号,选取方法是从随机数表第1行的第6列和第7列数字开始由左到右依次选取两个数字,则选出来的第6个红球的编号为( )
福利彩票“双色球”中,红球号码有编号为01,02,…,33的33个个体组成,某彩民利用下面的随机数表选取6组数作为6个红球的编号,选取方法是从随机数表第1行的第6列和第7列数字开始由左到右依次选取两个数字,则选出来的第6个红球的编号为( )| A、23 | B、09 | C、02 | D、17 |
已知两个单位向量
,
的夹角为60°,
=(1-t)
+t
,若
•
=-
,则实数t的取值是( )
| a |
| b |
| c |
| a |
| b |
| b |
| c |
| 1 |
| 2 |
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|