题目内容
等差数列{an}其前n项和为Sn.已知a3=6,S6=42,记bn=(-l)na
,设{bn}的前n项和为In,则T2n+1= .
| n(n+1) |
| 2 |
考点:等差数列的性质
专题:计算题,等差数列与等比数列
分析:利用a3=6,S6=42,求出a1=d=2,可得数列的通项,再分组求和,即可得出结论.
解答:
解:由题意,
,
∴a1=d=2,
∴an=2n,
∴a
=n(n+1),
∴bn=(-l)na
=(-l)nn(n+1),
∴T2n+1=-1×2+2×3+…+2n(2n+1)-(2n+1)(2n+2)=2(2+4+…+2n)-(2n+1)(2n+2)=-2n2-4n-2.
故答案为:-2n2-4n-2.
|
∴a1=d=2,
∴an=2n,
∴a
| n(n+1) |
| 2 |
∴bn=(-l)na
| n(n+1) |
| 2 |
∴T2n+1=-1×2+2×3+…+2n(2n+1)-(2n+1)(2n+2)=2(2+4+…+2n)-(2n+1)(2n+2)=-2n2-4n-2.
故答案为:-2n2-4n-2.
点评:本题考查等差数列的通项与求和,考查学生的计算能力,确定数列的通项是关键.

练习册系列答案
相关题目
执行如图的程序,若输入的x=2,则输出的所有x的值的和为( )


| A、6 | B、21 | C、101 | D、126 |
已知命题p:“若直线ax+y+1=0与直线ax-y+2=0垂直,则a=1”;命题q:“a
<b
”是“a<b”的充要条件,则( )
| 1 |
| 2 |
| 1 |
| 2 |
| A、p真,q假 |
| B、“p∧q”真 |
| C、“p∨q”真 |
| D、“p∨q”假 |
将函数f(x)=cos2x的图象向右平移
个单位后得到函数g(x),则g(x)具有性质( )
| π |
| 4 |
A、最大值为a,图象关于直线x=
| ||||
B、在(0,
| ||||
C、在(-
| ||||
D、周期为π,图象关于点(
|
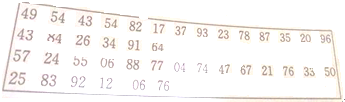 福利彩票“双色球”中,红球号码有编号为01,02,…,33的33个个体组成,某彩民利用下面的随机数表选取6组数作为6个红球的编号,选取方法是从随机数表第1行的第6列和第7列数字开始由左到右依次选取两个数字,则选出来的第6个红球的编号为( )
福利彩票“双色球”中,红球号码有编号为01,02,…,33的33个个体组成,某彩民利用下面的随机数表选取6组数作为6个红球的编号,选取方法是从随机数表第1行的第6列和第7列数字开始由左到右依次选取两个数字,则选出来的第6个红球的编号为( )| A、23 | B、09 | C、02 | D、17 |
设M、N是两个集合,定义M*N={x|x∈M,且x∉N}.若M={y|y=log2(-x2-2x+3)},N={y|y=
,x∈[0,9]},则M*N=( )
| x |
| A、(-∞,0] |
| B、(-∞,0) |
| C、[0,2] |
| D、(-∞,0)∪(2,3] |
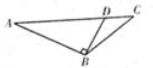
如图,在△ABC中,点D在AC上,AB⊥BD,BC=3
,BD=5,sin∠ABC=
,则CD的长为( )
| 3 |
2
| ||
| 5 |

A、
| ||
| B、4 | ||
C、2
| ||
| D、5 |