题目内容
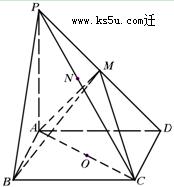
(本小题10分)如图,已知平行四边形ABCD和矩形ACEF所在的平面互相垂直, ,
,

(1)求证:AC⊥BF;
(2)求点A到平面FBD的距离.
 ,
,
(1)求证:AC⊥BF;
(2)求点A到平面FBD的距离.

(1)见解析(2)



本题考查异面直线垂直的证明、点到平面的距离.解题时要认真审题,仔细解答,注意向量法的合理运用.
(1)在△ACD中,由题设条件推导出CD⊥CA,由ABCD是平行四边形,知CA⊥AB,由直线垂直于平面的性质得到AC⊥BF.
(2)求出向量AD和平面FBD的法向量,用向量法能够求出点A到平面FBD的距离.
解法1:由
 得
得 ,故AD2=AC2+CD2,,,所以CD⊥CA
,故AD2=AC2+CD2,,,所以CD⊥CA
以CD为x轴,CA为y轴,以CE为z轴建立空间坐标系,
(1)C(0,0,0),D(1,0,0),A(0, ,0),F(0,
,0),F(0,  ,
, ),B(-1,
),B(-1, ,0),
,0),
 ,
, , ,
, ,
(2) ,
, 

由 ,
, 可得
可得 ,
,
点A到平面FBD的距离为d,


解法2 :(1)由
 得
得 ,故BC2=AC2+AB2,,,所以AC⊥AB
,故BC2=AC2+AB2,,,所以AC⊥AB
因为ACEF是矩形,AC⊥AF,所以AC⊥平面ABF,故AC⊥BF
(2)由 ,得
,得

(1)在△ACD中,由题设条件推导出CD⊥CA,由ABCD是平行四边形,知CA⊥AB,由直线垂直于平面的性质得到AC⊥BF.
(2)求出向量AD和平面FBD的法向量,用向量法能够求出点A到平面FBD的距离.
解法1:由

 得
得 ,故AD2=AC2+CD2,,,所以CD⊥CA
,故AD2=AC2+CD2,,,所以CD⊥CA以CD为x轴,CA为y轴,以CE为z轴建立空间坐标系,
(1)C(0,0,0),D(1,0,0),A(0,
 ,0),F(0,
,0),F(0,  ,
, ),B(-1,
),B(-1, ,0),
,0), ,
, , ,
, ,
(2)
 ,
, 

由
 ,
, 可得
可得 ,
,点A到平面FBD的距离为d,



解法2 :(1)由

 得
得 ,故BC2=AC2+AB2,,,所以AC⊥AB
,故BC2=AC2+AB2,,,所以AC⊥AB 因为ACEF是矩形,AC⊥AF,所以AC⊥平面ABF,故AC⊥BF
(2)由
 ,得
,得


练习册系列答案
相关题目
 .
.
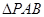 为边长为2的正三角形,底面ABCD为菱形,且平面PAB⊥平面ABCD,
为边长为2的正三角形,底面ABCD为菱形,且平面PAB⊥平面ABCD,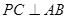 ,E为PD点上一点,满足
,E为PD点上一点,满足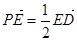
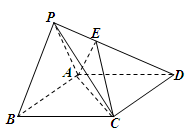
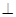 平面ABCD;
平面ABCD;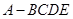 中,
中,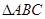 是正三角形,四边形
是正三角形,四边形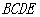 是矩形,且平面
是矩形,且平面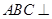 平面
平面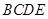 ,
,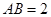 ,
,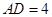 .
.
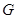 是
是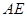 的中点,求证:
的中点,求证: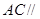 平面
平面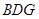 ;
;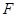 为线段
为线段 的中点,求二面角
的中点,求二面角 的正切值.
的正切值.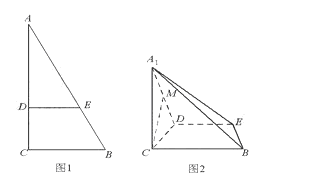
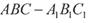 的侧棱与底面垂直,
的侧棱与底面垂直, ,MN分别是
,MN分别是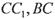 的中点,P点在
的中点,P点在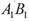 上,且满足
上,且满足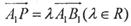
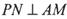
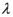 取何值时,直线PN与平面ABC所成的角
取何值时,直线PN与平面ABC所成的角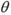 最大?并求出该最大角的正切值;
最大?并求出该最大角的正切值;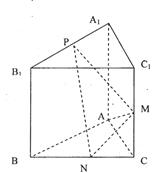
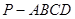 中,
中,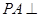 面
面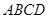 ,
,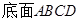 为菱形,且有
为菱形,且有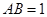 ,
,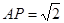 ,∠
,∠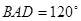 ,
,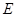 为
为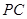 中点.
中点.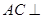 面
面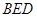 ;
;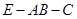 的平面角的余弦值.
的平面角的余弦值.
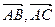 为一组邻边的平行四边形的面积S;
为一组邻边的平行四边形的面积S; 分别与向量
分别与向量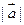 =
=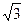 ,求向量
,求向量