题目内容
沿对角线AC将正方形ABCD折成直二面角后,AB与CD所在的直线所成的角等于( )
| A、90° | B、60° |
| C、45° | D、30° |
考点:异面直线及其所成的角
专题:空间角,空间向量及应用
分析:取AC中点O,连接BO,DO,容易说明OB,OC,OD两两垂直,所以可建立空间直角坐标系,分别求出A,B,C,D点的坐标,根据两向量夹角余弦公式的坐标运算求出向量
,
的夹角,从而求出直线AB,CD所成角.
| AB |
| CD |
解答:
解:学生取AC中点O,连接BO,DO,则:BO⊥AC,DO⊥AC;
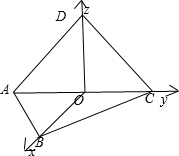 ∵B-AC-D是直二面角,∴∠BOD是该二面角的平面面角;
∵B-AC-D是直二面角,∴∠BOD是该二面角的平面面角;
∴∠BOD=90°,∴DO⊥BO;
∴分别以OB,OC,OD所在直线为x轴,y轴,z轴,建立空间直角坐标系,并设原正方形边长为1则:
A(0,-
,0),D(0,0,
),B(
,0,0),C(0,
,0);
∴
=(
,
,0),
=(0,-
,
);
设向量
,
的夹角为θ,则:cosθ=
=
=-
;
∴θ=120°,∴AB与CD所在的直线所成的角等于60°.
故选B.
 ∵B-AC-D是直二面角,∴∠BOD是该二面角的平面面角;
∵B-AC-D是直二面角,∴∠BOD是该二面角的平面面角;∴∠BOD=90°,∴DO⊥BO;
∴分别以OB,OC,OD所在直线为x轴,y轴,z轴,建立空间直角坐标系,并设原正方形边长为1则:
A(0,-
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
∴
| AB |
| ||
| 2 |
| ||
| 2 |
| CD |
| ||
| 2 |
| ||
| 2 |
设向量
| AB |
| CD |
| ||||
|
|
-
| ||
| 1 |
| 1 |
| 2 |
∴θ=120°,∴AB与CD所在的直线所成的角等于60°.
故选B.
点评:考查空间直角坐标系,二面角,直二面角,二面角的平面角,向量夹角的余弦公式的坐标运算.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若a>1,-2<b<-1,则函数y=ax+b的图象一定经过第( )象限.
| A、一、二、三 |
| B、一、三、四 |
| C、二、三、四 |
| D、一、二、四 |
若“?p且?q”与“?p或q”均为假命题,则( )
| A、p真q假 | B、p假q真 |
| C、p与q均真 | D、p与q均假 |
已知
⊥
,|
|=2,|
|=3,且向量3
+2
与k
-
互相垂直,则k的值为( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
A、-
| ||
B、
| ||
C、±
| ||
| D、1 |
抛物线y2=2px(p>0)的焦点为F,A为准线上一点,则线段FA的中垂线与抛物线的位置关系为( )
| A、相交 | B、相切 |
| C、相离 | D、以上都有可能 |
 如图所示,半径为3的圆中有一封闭曲线围成的阴影区域,在圆中随机撒一粒豆子,它落在阴影区域内的概率是
如图所示,半径为3的圆中有一封闭曲线围成的阴影区域,在圆中随机撒一粒豆子,它落在阴影区域内的概率是| 1 |
| 3 |
A、
| ||
| B、π | ||
| C、2π | ||
| D、3π |