题目内容
5.已知抛物线C:y2=mx(m>0)的焦点为F,点A(0,-$\sqrt{3}$),若射线FA与抛物线C相交于点M,与其准线相交于点D,且|FM|:|MD|=1:2,则点M的纵坐标为( )| A. | -$\frac{1}{3}$ | B. | -$\frac{\sqrt{3}}{3}$ | C. | -$\frac{2}{3}$ | D. | -$\frac{2\sqrt{3}}{3}$ |
分析 作出M在准线上的射影,根据|KM|:|MD|确定|KD|:|KM|的值,进而列方程求得m,再求出M的坐标
解答 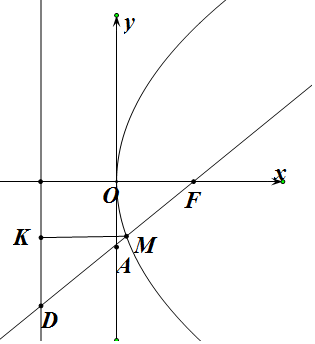 解:依题意F点的坐标为($\frac{m}{4}$,0),
解:依题意F点的坐标为($\frac{m}{4}$,0),
设M在准线上的射影为K,
由抛物线的定义知|MF|=|MK|,
∵|FM|:|MD|=1:2:
则|KD|:|KM|=$\sqrt{3}$:1,
kFD=$\sqrt{3}$,
kFD=$\frac{0+\sqrt{3}}{\frac{m}{4}-0}$=$\frac{4\sqrt{3}}{m}$
∴$\frac{4\sqrt{3}}{m}$=$\sqrt{3}$,求得m=4
∴直线FM的方程为y=$\sqrt{3}$(x-1),
与y2=4x,联立方程组,解得x=3(舍去)或x=$\frac{1}{3}$,
∴y2=$\frac{4}{3}$,
解y=-$\frac{2\sqrt{3}}{3}$或y=$\frac{2\sqrt{3}}{3}$(舍去),
故M的坐标为($\frac{1}{3}$,-$\frac{2\sqrt{3}}{3}$),
故选:D
点评 本题主要考查了抛物线的简单性质.抛物线中涉及焦半径的问题常利用抛物线的定义转化为点到准线的距离来解决.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
20.已知集合A={a,b,d},B={c,d},则A∪B等于( )
| A. | {d} | B. | {a,c} | C. | {a,b,c} | D. | {a,b,c,d} |
16.设曲线y=xn+1(n∈Z*)在点(1,1)处的切线与x轴的交点的横坐标为xn,则x1•x2•x3…•xn的值为( )
| A. | $\frac{1}{n}$ | B. | $\frac{n}{n+1}$ | C. | $\frac{1}{n+1}$ | D. | 1 |
10.在△ABC中,已知AB=$\sqrt{2}$,AC=$\sqrt{5}$,tan∠BAC=-3,则BC边上的高等于( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
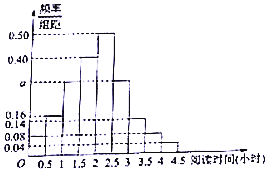 某校为了解高一学生周末的“阅读时间”,从高一年级中随机调查了100名学生进行调查,获得了每人的周末“阅读时间”(单位:小时),按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成样本的频率分布直方图如图所示.
某校为了解高一学生周末的“阅读时间”,从高一年级中随机调查了100名学生进行调查,获得了每人的周末“阅读时间”(单位:小时),按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成样本的频率分布直方图如图所示.