题目内容
15．设a＞0，若对于任意的x＞0，都有$\frac{1}{a}-\frac{1}{x}≤2x$，则a的取值范围是[$\frac{\sqrt{2}}{4}，+∞$）．分析 由对于任意的x＞0，都有$\frac{1}{a}-\frac{1}{x}≤2x$，转化为$\frac{1}{a}≤（\frac{1}{x}+2x）_{min}$，求出a的取值
解答 解：对于任意的x＞0，都有$\frac{1}{a}-\frac{1}{x}≤2x$，得到$\frac{1}{a}≤（\frac{1}{x}+2x）_{min}$，因为$\frac{1}{x}+2x≥2\sqrt{2}$，所以$\frac{1}{a}≤2\sqrt{2}$，解得a$≥\frac{\sqrt{2}}{4}$；
故答案为：[$\frac{\sqrt{2}}{4}，+∞$）．
点评 本题考查了恒成立的问题以及利用基本不等式求最值．
练习册系列答案
相关题目
5．已知抛物线C：y2=mx（m＞0）的焦点为F，点A（0，-$\sqrt{3}$），若射线FA与抛物线C相交于点M，与其准线相交于点D，且|FM|：|MD|=1：2，则点M的纵坐标为（ ）
| A． | -$\frac{1}{3}$ | B． | -$\frac{\sqrt{3}}{3}$ | C． | -$\frac{2}{3}$ | D． | -$\frac{2\sqrt{3}}{3}$ |
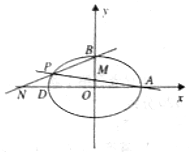已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$（a＞b＞0）的离心率为$\frac{1}{2}$，A（a，0），b（0，b），D（-a，0），△ABD的面积为$2\sqrt{3}$．