题目内容
10.若三条直线ax+y+3=0,x+y+2=0和2x-y+1=0相交于一点,则行列式$|\begin{array}{l}{a}&{1}\\{1}&{1}\end{array}|$的值为1.分析 先由三条直线ax+y+3=0,x+y+2=0和2x-y+1=0相交于一点,求出a,再由二阶行列式展开法则能求出$|\begin{array}{l}{a}&{1}\\{1}&{1}\end{array}|$的值.
解答 解:联立$\left\{\begin{array}{l}{x+y+2=0}\\{2x-y+1=0}\end{array}\right.$,得x=-1,y=-1,
∵三条直线ax+y+3=0,x+y+2=0和2x-y+1=0相交于一点,
∴直线ax+y+3=0过点(-1,-1),∴-a-1+3=0,解得a=2,
∴$|\begin{array}{l}{a}&{1}\\{1}&{1}\end{array}|$=a-1=2-1=1.
故答案为:1.
点评 本题考查二阶行列式的值的求法,是基础题,解题时要认真审题,注意二阶行列式展开法则的合理运用.

练习册系列答案
相关题目
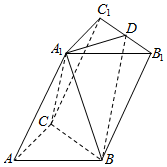 如图,在三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=2,AA1=4,A1在底面ABC的射影为BC的中点E,D是B1C1的中点.
如图,在三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=2,AA1=4,A1在底面ABC的射影为BC的中点E,D是B1C1的中点.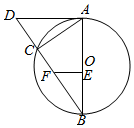 如图⊙O是Rt△ABC的外接圆,E、F是AB,BC上的点,且A,E,F,C四点共圆,延长BC至D,使得AC•BF=AD•BE.
如图⊙O是Rt△ABC的外接圆,E、F是AB,BC上的点,且A,E,F,C四点共圆,延长BC至D,使得AC•BF=AD•BE.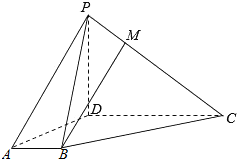 如图,四棱锥P-ABCD中,PD⊥底面ABCD,AB∥CD,∠BAD=$\frac{π}{3}$,AB=1,CD=3,M为PC上一点,MC=2PM.
如图,四棱锥P-ABCD中,PD⊥底面ABCD,AB∥CD,∠BAD=$\frac{π}{3}$,AB=1,CD=3,M为PC上一点,MC=2PM. 如图,在平行六面体ABCD-A1B1C1D1中,AC与BD的交点为点M.设$\overrightarrow{{C_1}{D_1}}=\overrightarrow a$,$\overrightarrow{{C_1}{B_1}}=\overrightarrow b$,$\overrightarrow{{C_1}C}=\overrightarrow c$,用$\overrightarrow a$,$\overrightarrow b$,$\overrightarrow c$表示向量$\overrightarrow{M{B_1}}$,则$\overrightarrow{M{B}_{1}}$=-$\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$-$\overrightarrow{c}$.
如图,在平行六面体ABCD-A1B1C1D1中,AC与BD的交点为点M.设$\overrightarrow{{C_1}{D_1}}=\overrightarrow a$,$\overrightarrow{{C_1}{B_1}}=\overrightarrow b$,$\overrightarrow{{C_1}C}=\overrightarrow c$,用$\overrightarrow a$,$\overrightarrow b$,$\overrightarrow c$表示向量$\overrightarrow{M{B_1}}$,则$\overrightarrow{M{B}_{1}}$=-$\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$-$\overrightarrow{c}$.