题目内容
12.在锐角△ABC中,a、b、c分别为角A、B、C所对的边,且$\sqrt{3}b=2csinB$(Ⅰ)确定角C的大小;
(Ⅱ)若c=$\sqrt{7}$,且a+b=5,求△ABC的面积.
分析 (Ⅰ)由已知等式结合正弦定理求得sinC的值,进一步求得C;
(Ⅱ)由余弦定理结合已知c=$\sqrt{7}$,且a+b=5求得ab=6,代入三角形面积公式得答案.
解答 解:(Ⅰ)由$\sqrt{3}b=2csinB$及正弦定理得,
$\sqrt{3}•2R•sinB=2•2R•sinCsinB…(1)$,①
∵sinB≠0,∴sinC=$\frac{\sqrt{3}}{2}$,
又△ABC是锐角三角形,∴$C=\frac{π}{3}$;
(Ⅱ)由余弦定理得:${a}^{2}+{b}^{2}-2ab•cos\frac{π}{3}=7$,即a2+b2-ab=7,②
由②变形得(a+b)2-3ab=7,
∵a+b=5,∴ab=6,
∴${S_{△ABC}}=\frac{1}{2}absinC=\frac{1}{2}×6×\frac{{\sqrt{3}}}{2}=\frac{{3\sqrt{3}}}{2}$.
点评 本题考查三角形的解法,考查了正弦定理和余弦定理在解三角形中的应用,是中档题.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
2.为了了解高一、高二、高三的身体状况,现用分层抽样的方法抽出一个容量为1200的样本,三个年级学生数之比依次为k:5:3,已知高一年级共抽取了240人,则高三年级抽取的人数为( )
| A. | 240 | B. | 300 | C. | 360 | D. | 400 |
3.椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的短轴长为( )
| A. | 2$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | 4 | D. | 2 |
20.过点M(2,-1)作斜率为$\frac{1}{2}$的直线与椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)相交于A,B两个不同点,若M是AB的中点,则该椭圆的离心率e=( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{3}{4}$ |
7.中石化集团通过与安哥拉国家石油公司合作,获得了安哥拉深海油田区块的开采权,集团在某些区块随机初步勘探了部分口井,取得了地质资料.进入全面勘探时期后,集团按网络点来布置井位进行全面勘探.由于勘探一口井的费用很高,如果新设计的井位与原有井位重合或接近,便利用旧井的地质资料,不必打这口新井.以节约勘探费用.若口井勘探初期数据资料见如表:
(Ⅰ)1~6号旧井位置线性分布,借助前5组数据求得回归直线方程为y=6.5x+a,求a,并估计y的预报值;
(Ⅱ)现准备勘探新井7(1,25),若通过1、3、5、7号井计算出的$\widehatb,\widehata$的值与(I)中b,a的值差不超过10%,则使用位置最迫近的已有旧井6(1,y),否则在新位置打开,请判断可否使用旧井?($\widehatb=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n_x^{-2}}}},\widehata=\overline y-\widehatb\overline x,\sum_{i=1}^4{{x_{2i-1}}^2=94,\sum_{i=1}^4{{x_{2i-1}}{y_{2i-1}}=945}}$)
(Ⅲ)设口井出油量与勘探深度的比值k不低于20的勘探并称为优质井,那么在原有6口井中任意勘探4口井,求勘探优质井数X的分布列与数学期望.
| 井号I | 1 | 2 | 3 | 4 | 5 | 6 |
| 坐标(x,y)(km) | (2,30) | (4,40) | (5,60) | (6,50) | (8,70) | (1,y) |
| 钻探深度(km) | 2 | 4 | 5 | 6 | 8 | 10 |
| 出油量(L) | 40 | 70 | 110 | 90 | 160 | 205 |
(Ⅱ)现准备勘探新井7(1,25),若通过1、3、5、7号井计算出的$\widehatb,\widehata$的值与(I)中b,a的值差不超过10%,则使用位置最迫近的已有旧井6(1,y),否则在新位置打开,请判断可否使用旧井?($\widehatb=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n_x^{-2}}}},\widehata=\overline y-\widehatb\overline x,\sum_{i=1}^4{{x_{2i-1}}^2=94,\sum_{i=1}^4{{x_{2i-1}}{y_{2i-1}}=945}}$)
(Ⅲ)设口井出油量与勘探深度的比值k不低于20的勘探并称为优质井,那么在原有6口井中任意勘探4口井,求勘探优质井数X的分布列与数学期望.
17.下列命题成立的是( )
| A. | 如果a>b,c≠0,那么$\frac{a}{c}>\frac{b}{c}$ | B. | 如果a>b,那么a2>b2 | ||
| C. | 如果a>b,c>d,那么a+d>b+c | D. | 如果a>b,c>d,那么a-d>b-c |
4. 如图,正四棱台ABCD-A1B1C1D1的上底面边长为1,下底面边长为3,高为1,M为BC的中点,则直线B1M与平面ACC1A1的夹角的正弦值为( )
如图,正四棱台ABCD-A1B1C1D1的上底面边长为1,下底面边长为3,高为1,M为BC的中点,则直线B1M与平面ACC1A1的夹角的正弦值为( )
 如图,正四棱台ABCD-A1B1C1D1的上底面边长为1,下底面边长为3,高为1,M为BC的中点,则直线B1M与平面ACC1A1的夹角的正弦值为( )
如图,正四棱台ABCD-A1B1C1D1的上底面边长为1,下底面边长为3,高为1,M为BC的中点,则直线B1M与平面ACC1A1的夹角的正弦值为( )| A. | $\frac{\sqrt{2}}{3}$ | B. | $\frac{\sqrt{2}}{6}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{3}}{6}$ |
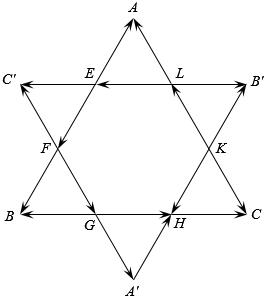 如图所示,△ABC和△A′B′C′是在各边的$\frac{1}{3}$处相交的两个全等的正三角形,设△ABC的边长为a,图中列出了长度均为$\frac{a}{3}$的若干个向量,求:
如图所示,△ABC和△A′B′C′是在各边的$\frac{1}{3}$处相交的两个全等的正三角形,设△ABC的边长为a,图中列出了长度均为$\frac{a}{3}$的若干个向量,求: