题目内容
已知圆C:x2+y2-4x-6y+4=0
(1)过点A(-1,-1)作圆C的切线l1,求切线l1的方程;
(2)不论实数m为何值,证明直线l2:mx-y-3m+2=0与圆C总相交;
(3)若直线l2:被圆C截得的弦为AB,求AB的最小值.
(1)过点A(-1,-1)作圆C的切线l1,求切线l1的方程;
(2)不论实数m为何值,证明直线l2:mx-y-3m+2=0与圆C总相交;
(3)若直线l2:被圆C截得的弦为AB,求AB的最小值.
考点:圆的切线方程,直线与圆的位置关系
专题:计算题,直线与圆
分析:(1)根据题意,可得圆心为(2,3),半径r=3.设切线l1的斜率为k,利用点到直线的距离公式建立关于k的等式,解出k=
.再根据直线l1过点A且斜率不存在时也与圆C相切,可得满足条件的切线l1的方程.
(2)化简直线l2得:m(x-3)-(y-2)=0,可知直线l2经过定点P(3,2),而点P恰好是圆C内部的一个定点,由此可得不论实数m为何值,直线l2与圆C总相交;
(3)根据圆的性质,可知当圆心C与P的连线与直线l2互相垂直时,直线l2被圆C截得的弦AB有最小值.由此利用两点的距离公式与垂径定理,即可求出AB的最小值.
| 7 |
| 24 |
(2)化简直线l2得:m(x-3)-(y-2)=0,可知直线l2经过定点P(3,2),而点P恰好是圆C内部的一个定点,由此可得不论实数m为何值,直线l2与圆C总相交;
(3)根据圆的性质,可知当圆心C与P的连线与直线l2互相垂直时,直线l2被圆C截得的弦AB有最小值.由此利用两点的距离公式与垂径定理,即可求出AB的最小值.
解答:
解:(1)将圆C化成标准方程,得(x-2)2+(y-3)2=9,
∴圆心为C(2,3),半径r=3.
设过点A(-1,-1)的圆C的切线l1方程为y+1=k(x+1),
即kx-y+k-1=0,
则点C到直线l1的距离等于半径,
即
=3,
解之得k=
,直线l1的方程为y+1=
(x+1),
即y=
x-
.
又∵当经过点A的直线斜率不存在时,
直线x=-1到点C的距离也等于半径,此时直线与圆C也相切.
∴经过点A(-1,-1)并且与圆C相切的直线l1的方程为y=
x-
或x=-1;
(2)化简直线l2:mx-y-3m+2=0,得m(x-3)-(y-2)=0,
∴直线l2经过直线x-3=0与直线y-2=0的交点P(3,2),
∵点P(3,2)满足3-2)2+(2-3)2<9,∴点P(3,2)是圆C内部一点.
由于直线l2经过圆C内部的定点P(3,2),所以不论实数m为何值,直线l2与圆C总相交;
(3)由(2)知直线l2经过圆C内部的点P(3,2),
∴由圆的性质,当直线l2与CP互相垂直时,l2被圆C截得的弦AB有最小值.
∵|PC|=
=
,
∴根据垂径定理,得|AB|=2
=2
,
即直线l2被圆C截得的弦AB长的最小值为2
.
∴圆心为C(2,3),半径r=3.
设过点A(-1,-1)的圆C的切线l1方程为y+1=k(x+1),
即kx-y+k-1=0,
则点C到直线l1的距离等于半径,
即
| |2k-3+k-1| | ||
|
解之得k=
| 7 |
| 24 |
| 7 |
| 24 |
即y=
| 7 |
| 24 |
| 17 |
| 24 |
又∵当经过点A的直线斜率不存在时,
直线x=-1到点C的距离也等于半径,此时直线与圆C也相切.
∴经过点A(-1,-1)并且与圆C相切的直线l1的方程为y=
| 7 |
| 24 |
| 17 |
| 24 |
(2)化简直线l2:mx-y-3m+2=0,得m(x-3)-(y-2)=0,
∴直线l2经过直线x-3=0与直线y-2=0的交点P(3,2),
∵点P(3,2)满足3-2)2+(2-3)2<9,∴点P(3,2)是圆C内部一点.
由于直线l2经过圆C内部的定点P(3,2),所以不论实数m为何值,直线l2与圆C总相交;
(3)由(2)知直线l2经过圆C内部的点P(3,2),
∴由圆的性质,当直线l2与CP互相垂直时,l2被圆C截得的弦AB有最小值.
∵|PC|=
| (3-2)2+(2-3)2 |
| 2 |
∴根据垂径定理,得|AB|=2
| r2-|PC|2 |
| 7 |
即直线l2被圆C截得的弦AB长的最小值为2
| 7 |
点评:本题已知圆C的方程,求圆C经过定点的切线方程,并求直线被圆截得弦长的最小值.着重考查了直线的方程、直线与圆的位置关系、点与圆的位置关系、点到直线的距离公式和圆的有关性质等知识,属于中档题.

练习册系列答案
相关题目
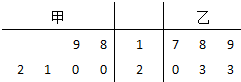 甲、乙两人同时生产一种产品,6天中,完成的产量茎叶图(茎表示十位,叶表示个位)如图所示:
甲、乙两人同时生产一种产品,6天中,完成的产量茎叶图(茎表示十位,叶表示个位)如图所示: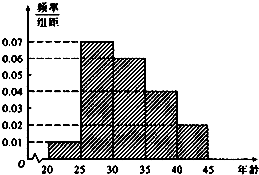 某市为增强市民的环境保护意识,面向全市征召义务宣传志愿者.现从符合条件的志愿者中随机抽取100名按年龄分组:第1组[20,25),第2组[25,30),第3组[30,35),第4组[35,40),第5组[40,45],得到的频率分布直方图如图所示.
某市为增强市民的环境保护意识,面向全市征召义务宣传志愿者.现从符合条件的志愿者中随机抽取100名按年龄分组:第1组[20,25),第2组[25,30),第3组[30,35),第4组[35,40),第5组[40,45],得到的频率分布直方图如图所示.