题目内容
8.在平行四边形ABCD中,AB=$\frac{1}{2}$BC=1,∠BAD=120°,$\overrightarrow{BE}$=$\frac{1}{2}$$\overrightarrow{BC}$,则$\overrightarrow{AC}$•$\overrightarrow{DE}$=( )| A. | -$\frac{7}{2}$ | B. | -$\frac{5}{2}$ | C. | -$\frac{3}{2}$ | D. | -$\frac{1}{2}$ |
分析 根据平面向量的线性运算法则与数量积的定义,计算即可.
解答 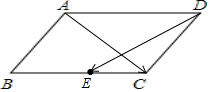 解:如图所示,平行四边形ABCD中,
解:如图所示,平行四边形ABCD中,
AB=$\frac{1}{2}$BC=1,∠BAD=120°,$\overrightarrow{BE}$=$\frac{1}{2}$$\overrightarrow{BC}$;
∴$\overrightarrow{AC}$=$\overrightarrow{AB}$+$\overrightarrow{AD}$,
$\overrightarrow{DE}$=$\overrightarrow{DC}$+$\overrightarrow{CE}$=$\overrightarrow{AB}$-$\frac{1}{2}$$\overrightarrow{AD}$,
∴$\overrightarrow{AC}$•$\overrightarrow{DE}$=($\overrightarrow{AB}$+$\overrightarrow{AD}$)•($\overrightarrow{AB}$-$\frac{1}{2}$$\overrightarrow{AD}$)
=${\overrightarrow{AB}}^{2}$+$\frac{1}{2}$$\overrightarrow{AB}$•$\overrightarrow{AD}$-$\frac{1}{2}$${\overrightarrow{AD}}^{2}$
=12+$\frac{1}{2}$×1×2×cos120°-$\frac{1}{2}$×22
=-$\frac{3}{2}$.
故选:C.
点评 本题考查了平面向量数量积的定义与线性运算法则的应用问题,是基础题.

练习册系列答案
相关题目
14.z=$\frac{5i}{1-2i}$(i是虚数单位),则z为( )
| A. | 2-i | B. | 2+i | C. | -2-i | D. | -2+i |
15.设a,b∈R,则“a+b>4”是“a>1且b>3”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
13.已知数列{an},{bn}满足a1=1,且an,an+1是方程x2-bnx+3n=0的两根,则b8等于( )
| A. | 54 | B. | 108 | C. | 162 | D. | 324 |
17.已知全集U={1,3,5,7,9},集合A={1,5},B={3,5},则∁UA∩∁UB=( )
| A. | {7,9} | B. | {1,3,7,9} | C. | {5} | D. | {1,3,5} |
18.设命题甲:关于x的不等式x2+2ax+4≤0有解,命题乙:设函数f(x)=loga(x+a-2)在区间(1,+∞)上恒为正值,那么甲是乙的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |