题目内容
已知a，b，c∈R∈尺，则下列命题正确的是（ ）
| A、a＞b⇒ac2＞bc2 | |||||||||
B、
| |||||||||
C、
| |||||||||
D、
|
考点：不等式的基本性质
专题：不等式的解法及应用
分析：A．c=0时，不成立；
B．c＜0时，不成立；
C．由a＞b，ab＜0，利用不等式的基本性质可得
＜
，化简即可；
D．由a＞b，ab＞0，利用不等式的基本性质可得
＞
，化简即可得出．
B．c＜0时，不成立；
C．由a＞b，ab＜0，利用不等式的基本性质可得
| a |
| ab |
| b |
| ab |
D．由a＞b，ab＞0，利用不等式的基本性质可得
| a |
| ab |
| b |
| ab |
解答：
解：A．c=0时，不成立；
B．c＜0时，不成立；
C．∵a＞b，ab＜0，∴
＜
，化为
＜
，正确；
D．∵a＞b，ab＞0，∴
＞
，化为
＞
，不正确．
故选：C．
B．c＜0时，不成立；
C．∵a＞b，ab＜0，∴
| a |
| ab |
| b |
| ab |
| 1 |
| b |
| 1 |
| a |
D．∵a＞b，ab＞0，∴
| a |
| ab |
| b |
| ab |
| 1 |
| b |
| 1 |
| a |
故选：C．
点评：本题考查了不等式的基本性质，考查了推理能力与计算能力，属于基础题．
练习册系列答案
相关题目
用a，b，c表示三条不同的直线，γ表示平面，给出下列命题：
①若a∥b，b∥c，则a∥c； ②若a⊥b，b⊥c，则a⊥c；
③若a∥γ，b∥γ，则a∥b； ④若a⊥γ，b⊥γ，则a∥b．其中真命题的序号是（ ）
①若a∥b，b∥c，则a∥c； ②若a⊥b，b⊥c，则a⊥c；
③若a∥γ，b∥γ，则a∥b； ④若a⊥γ，b⊥γ，则a∥b．其中真命题的序号是（ ）
| A、①② | B、②③ | C、①④ | D、③④ |
函数f（x）=
的值域为（ ）
|
A、[-
| ||||||||
B、[
| ||||||||
C、[0，
| ||||||||
D、[0，
|
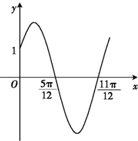已知函数f（x）=Asin（ωx+φ）（x∈R，ω＞0，0＜φ＜