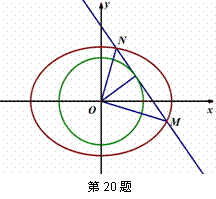
题目内容
如图,已知点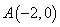 ,点
,点 是
是 上任意一点,线段
上任意一点,线段 的垂直平分线交
的垂直平分线交 于点
于点 ,点
,点 的轨迹记为曲线
的轨迹记为曲线 .
.
(1)求曲线 的方程;
的方程;
(2)已知 的切线
的切线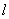 总与曲线
总与曲线 有两个交点
有两个交点 ,当
,当 ,求
,求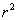 的取值范围。
的取值范围。
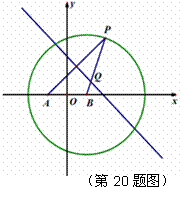
(1)由题意,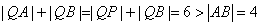 ,
,
根据椭圆的定义,Q点轨迹是以A、B为焦点的椭圆,且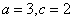 ,………………2分
,………………2分
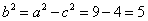
∴曲线C的轨迹方程是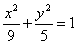 .………………4分
.………………4分
(2)先考虑切线的斜率存在的情形. 设切线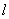 :
: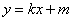 ,则
,则
由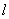 与⊙O相切得
与⊙O相切得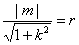 即
即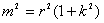 ①……………6分
①……………6分
 由
由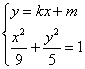 ,消去
,消去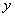 得,
得,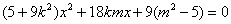 ,
,
设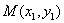 ,
,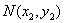 ,则由韦达定理得
,则由韦达定理得
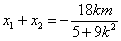 ,
,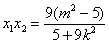 ……………8分
……………8分
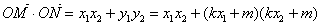
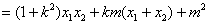
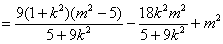
 ②……………………10分
②……………………10分
由于满足 ,对此
,对此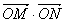
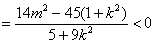
结合①式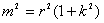 可得
可得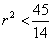 …………………………………………12分
…………………………………………12分
最后考虑特殊情况:
当满足 的那条切线斜率不存在时,切线方程为
的那条切线斜率不存在时,切线方程为
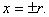 代入椭圆方程可得交点的纵坐标
代入椭圆方程可得交点的纵坐标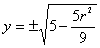 ,因
,因 ,故
,故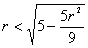 ,得到
,得到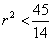

练习册系列答案
相关题目
某网站体育版块足球栏目组发起了“射手的上一场进球与本场进球有无关系”的调查活动,在所有参与调查的人中,持“有关系”“无关系”“不知道”态度的人数如表所示:
| 有关系 | 无关系 | 不知道 | |
| 人数 | 500 | 600 | 900 |
(1)在所有参与调查的人中,用分层抽样的方法抽取样本,已知从持“有关系”态度的人中抽取了5人,求总样本容量。
(2)持“有关系”态度的人中,40岁以下和40岁以上(含40岁)的比例为2:3,从抽取的5个样本中,再任选2人作访问,求至少1人在40岁以下的概率;
 过圆
过圆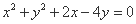 的圆心,则
的圆心,则 ________.
________.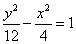 的顶点为焦点,长半轴长为4的椭圆方程为( )
的顶点为焦点,长半轴长为4的椭圆方程为( )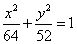 B.
B.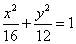 C.
C.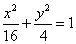 D.
D.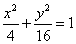
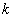 的值是( )
的值是( )

 内有零点且单调递增的是
内有零点且单调递增的是 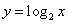 B.
B.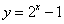 C.
C.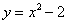 D.
D.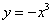
 成立的实数a的范围是 .
成立的实数a的范围是 .