题目内容
5．设i为虚数单位，复数z满足$\frac{1+i}{z}$=1-i，则复数z=（ ）| A． | 2i | B． | -2i | C． | i | D． | -i |
分析 利用复数的运算法则即可得出．
解答 解：$\frac{1+i}{z}$=1-i，
则复数z=$\frac{1+i}{1-i}$=$\frac{（1+i）^{2}}{（1-i）（1+i）}$=$\frac{2i}{2}$=i．
故选：C．
点评 本题考查了复数的运算法则，考查了推理能力与计算能力，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
15．已知全集U=R，集合A={x||x|≤1}，B={x|x≤1}，则（∁UA）∩B等于（ ）
| A． | {x|x≤-1} | B． | {x|x＜-1} | C． | {-1} | D． | {x|-1＜x|≤1} |
13．复数z=$\frac{（1+i）（2-i）}{-i}$（i为虚数单位）的虚部为（ ）
| A． | -1 | B． | -i | C． | 3 | D． | 3i |
20．复数z=（$\frac{i}{1-i}$）2（i为虚数单位），则复数z+1在复平面上对应的点位于（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
10．
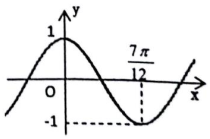设函数y=sinωx（ω＞0）的最小正周期是T，将其图象向左平移$\frac{1}{4}$T后，得到的图象如图所示，则函数y=sinωx（ω＞0）的单增区间是（ ）
设函数y=sinωx（ω＞0）的最小正周期是T，将其图象向左平移$\frac{1}{4}$T后，得到的图象如图所示，则函数y=sinωx（ω＞0）的单增区间是（ ）| A． | [$\frac{7kπ}{6}$-$\frac{7π}{24}$，$\frac{7kπ}{6}$+$\frac{7π}{24}$]（k∈Z） | B． | [$\frac{7kπ}{3}$-$\frac{7π}{24}$，$\frac{7kπ}{3}$+$\frac{7π}{24}$]（k∈Z） | ||
| C． | [$\frac{7kπ}{3}$-$\frac{7π}{12}$，$\frac{7kπ}{3}$+$\frac{7π}{12}$]（k∈Z） | D． | [$\frac{7kπ}{6}$+$\frac{7π}{24}$，$\frac{7kπ}{6}$+$\frac{21π}{24}$]（k∈Z） |
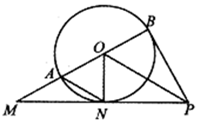如图所示，已知AB为⊙O的直径，PB、PN都是⊙O的切线，切点分别为B、N，PN交BA的延长线于点M．