题目内容
3.已知直线l1:x+y-2=0,直线l2过点A(-2,0)且与直线l1平行.(1)求直线l2的方程;
(2)点B在直线l1上,若|AB|=4,求点B的坐标.
分析 (1)由题意得l1的斜率为-1,即可求直线l2的方程;
(2)设B(x0,y0),则由点B在直线l1上得,x0+y0-2=0①,由|AB|=4得,$\sqrt{{{({{x_0}+2})}^2}+{y_0}^2}=4$②,联立①②,求点B的坐标.
解答 解:(1)由题意得l1的斜率为-1,…(2分)
则直线l2的方程为y+2=-x即x+y+2=0.…(5分)
(2)设B(x0,y0),则由点B在直线l1上得,x0+y0-2=0①…(7分)
由|AB|=4得,$\sqrt{{{({{x_0}+2})}^2}+{y_0}^2}=4$②…(10分)
联立①②解得,$\left\{\begin{array}{l}{x_0}=2\\{y_0}=0\end{array}\right.$或$\left\{\begin{array}{l}{x_0}=-2\\{y_0}=4\end{array}\right.$
即点B的坐标为B(2,0)或B(-2,4).…(14分)
点评 本题考查直线方程,考查直线与直线的位置关系,考查学生的计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.设点F1、F2是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点(O为坐标原点),以O为圆心,|F1F2|为直径的圆交双曲线于点M(第一象限).若过点M作x轴的垂线,垂足恰为线段OF2的中点,则双曲线的离心率是( )
| A. | $\sqrt{3}$-1 | B. | $\sqrt{3}$ | C. | $\sqrt{3}$+1 | D. | 2 |
8.函数y=ax+1(a>0,a≠1)的图象必经过点( )
| A. | (0,1) | B. | (1,0) | C. | (0,2) | D. | (2,1) |

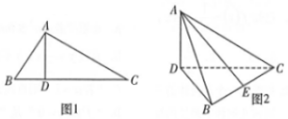 如图1,在Rt△ABC中,∠ABC=60°,AD是斜边BC上的高,沿AD将△ABC折成60°的二面角B-AD-C,如图2.
如图1,在Rt△ABC中,∠ABC=60°,AD是斜边BC上的高,沿AD将△ABC折成60°的二面角B-AD-C,如图2.