题目内容
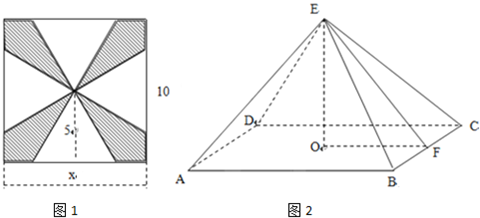
已知∠BAD=90°的等腰△ABD与正△CBD所在平面成60°的二面角，则AB与平面BCD所成角的大小为 ．
考点：直线与平面所成的角
专题：空间角
分析：过A做BD垂线，垂足为E，这时，AE垂直BD，过A做面BCD的垂线，垂足为F，∠ABF是AB与平面BCD所成角，由此能求出AB与平面BCD所成角的大小．
解答：
解：过A做BD垂线，垂足为E，
这时，AE垂直BD，
所以过A做面BCD的垂线，垂足为F，
则∠ABF是AB与平面BCD所成角，
∵∠BAD=90°的等腰△ABD与正△CBD所在平面成60°的二面角，
∴AF=AEsin60°=
AE，AB=
AE，
sin∠ABF=
=
=
，
∴AB与平面BCD所成角的大小为arcsin
．
故答案为：arcsin
．
这时，AE垂直BD，
所以过A做面BCD的垂线，垂足为F，
则∠ABF是AB与平面BCD所成角，
∵∠BAD=90°的等腰△ABD与正△CBD所在平面成60°的二面角，
∴AF=AEsin60°=
| ||
| 2 |
| 2 |
sin∠ABF=
| AF |
| AB |
| ||||
|
| ||
| 4 |
∴AB与平面BCD所成角的大小为arcsin
| ||
| 4 |
故答案为：arcsin
| ||
| 4 |
点评：本题考查直线与平面所成角的大小的求法，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
备战中考寒假系列答案
相关题目
