题目内容
截至到1999年底,我国人口约为13亿.如果今后能将人口年平均增长率控制在1%.
(1)那么在过20年后,我过人口数最多为多少?(精确到亿)
(2)再过多少年我过人口总数达到18亿?(取整数)
参考数据如下:
1.0119=1.208,1.0120=1.22,1.0121=1.232
log1018=1.2553,log1013=1.1139,log101.01=0.0043.
(1)那么在过20年后,我过人口数最多为多少?(精确到亿)
(2)再过多少年我过人口总数达到18亿?(取整数)
参考数据如下:
1.0119=1.208,1.0120=1.22,1.0121=1.232
log1018=1.2553,log1013=1.1139,log101.01=0.0043.
考点:等比数列的通项公式
专题:函数的性质及应用,等差数列与等比数列
分析:(1)首先根据题意建立等比关系式,最后求的结果.
(2)根据题意建立方程,利用对数求出结果.
(2)根据题意建立方程,利用对数求出结果.
解答:
解:(1)已知人口年平均增长率为1%,则由题意可得,每一年的人口数量构成一个等比数列公比为(1+1%),则由题意那么在过20年后,我过人口数最多为:13(1+1%)20=15.86亿
(2)设经过x年我过人口总数达到18亿,则根据题意得到:13(1+1%)x=18
两边取对数:lg13+xlg1.01=lg18
解得:x≈35
(2)设经过x年我过人口总数达到18亿,则根据题意得到:13(1+1%)x=18
两边取对数:lg13+xlg1.01=lg18
解得:x≈35
点评:本题考查的知识要点:等比数列的通项公式在实际问题中的应用,对数的运算问题.

练习册系列答案
相关题目
若a<b<c,函数f(x)=(x-a)(x-b)+(x-b)(x-c)+(x-a)(x-c)的零点在区间( )上.
| A、(-∞,a),(a,b) |
| B、(a,b),(b,c) |
| C、(a,c),(c,+∞) |
 如图,在四棱椎P-ABCD中,PD⊥平面ABCD,CD∥AB,CD⊥DA且PD=DA=AB=
如图,在四棱椎P-ABCD中,PD⊥平面ABCD,CD∥AB,CD⊥DA且PD=DA=AB=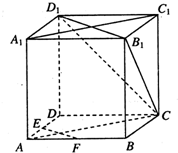 如图,在正方体ABCD-A1B1C1D1中,E、F分别为AD,AB的中点.
如图,在正方体ABCD-A1B1C1D1中,E、F分别为AD,AB的中点.