题目内容
8.己知向量$\overrightarrow{a}$=($\sqrt{2}$,$-\sqrt{2}$),$\overrightarrow{b}$=(cosx,sinx),x∈(0,$\frac{π}{2}$).(I)若向量$\overrightarrow{a}$与$\overrightarrow{b}$平行,求tanx的值;
(Ⅱ)若向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为$\frac{π}{3}$,求x的值.
分析 (I)向量$\overrightarrow{a}$与$\overrightarrow{b}$平行,可得$\sqrt{2}$sinx+$\sqrt{2}$cosx=0,化简即可得出;
(II)$\overrightarrow{a}•\overrightarrow{b}$=$\sqrt{2}cosx$-$\sqrt{2}$sinx,$|\overrightarrow{a}|$=2,$|\overrightarrow{b}|$=1.可得$cos\frac{π}{3}$=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}$=$\frac{\sqrt{2}cosx-\sqrt{2}sinx}{2}$=$\frac{1}{2}$,化简即可得出.
解答 解:(I)∵向量$\overrightarrow{a}$与$\overrightarrow{b}$平行,∴$\sqrt{2}$sinx+$\sqrt{2}$cosx=0,化为tanx=-1;
(II)∵$\overrightarrow{a}•\overrightarrow{b}$=$\sqrt{2}cosx$-$\sqrt{2}$sinx,$|\overrightarrow{a}|$=2,$|\overrightarrow{b}|$=1.
∴$cos\frac{π}{3}$=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}$=$\frac{\sqrt{2}cosx-\sqrt{2}sinx}{2}$=$\frac{1}{2}$,
∴$\sqrt{2}$cosx-$\sqrt{2}$sinx=1,∴$sin(\frac{π}{4}-x)$=$\frac{1}{2}$,
∵x∈(0,$\frac{π}{2}$),∴$(\frac{π}{4}-x)$∈$(-\frac{π}{4},\frac{π}{4})$.
∴$\frac{π}{4}$-x=$\frac{π}{6}$,
解得x=$\frac{π}{12}$.
点评 本题考查了向量共线定理、向量的夹角公式、三角函数求值,考查了推理能力与计算能力,属于中档题.

| A. | 90 | B. | 115 | C. | 210 | D. | 385 |
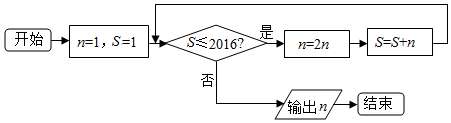
| A. | 10 | B. | 11 | C. | 1024 | D. | 2048 |