题目内容

16．求和：求数列{n+$\frac{1}{{2}^{n}}$}的前n项和．

分析 利用等差数列与等比数列的前n项和公式即可得出．

解答 解：数列{n+$\frac{1}{{2}^{n}}$}的前n项和=（1+2+…+n）+$（\frac{1}{2}+\frac{1}{{2}^{2}}+…+\frac{1}{{2}^{n}}）$
=$\frac{n（n+1）}{2}$+$\frac{\frac{1}{2}（1-\frac{1}{{2}^{n}}）}{1-\frac{1}{2}}$
=$\frac{n（n+1）}{2}$+1-$\frac{1}{{2}^{n}}$．

点评 本题考查了等差数列与等比数列的前n项和公式，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
6．已知函数f（x）的定义域为实数集R，
（1）若函数f（x）=2xsin（πx），证明f（x+2）=4f（x）；
（2）若f（x+T）=kf（x）（k＞0，T＞0），若f（x）=axφ（x）（其中a为正的常数），试证明函数φ（x）是以T为周期的周期函数；
（3）若f（x+6）=$\sqrt{2}$f（x），且当x∈[-3，3]时，f（x）=$\frac{1}{10}$x（x2-9），记Sn=f（2）+f（6）+f（10）+…+f（4n-2）n∈N*，求使得S1、S2、S3…Sn小于1000都成立的最大整数n．
7．若函数f（x）=mx+$\sqrt{x}$在区间[$\frac{1}{2}$，1]上单调递增，则（　　）
A．[-$\frac{1}{2}$，+∞）B．[$\frac{1}{2}$，+∞）C．[-2，+∞）D．[2，+∞）
4．奇函数y=f（x）（x∈R）的图象必过定点（0，0）．
11．等比数列{an}的前n项和为Sn，若S3=2，S6=10．则S9等于42．
1．已知f0（x）=cosxsinx，f1（x）=f0′（x），f2（x）=f1′（x），f3（x）=f2′（x），fn（x）=fn-1′（x），n∈N+，则f2016（x）等于（　　）
A．sin22015xB．2cosxsinxC．-22015cos2xD．22015sin2x
8．己知向量$\overrightarrow{a}$=（$\sqrt{2}$，$-\sqrt{2}$），$\overrightarrow{b}$=（cosx，sinx），x∈（0，$\frac{π}{2}$）．
（I）若向量$\overrightarrow{a}$与$\overrightarrow{b}$平行，求tanx的值；
（Ⅱ）若向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为$\frac{π}{3}$，求x的值．
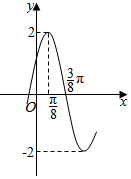5．函数f（x）=2sin（ωx+φ），（ω＞0，0＜φ＜$\frac{π}{2}$）的部分图象如图所示，求ω，φ的值．
8．数列{an}前n项和Sn=2n，则a3+a4=12．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网