题目内容
14. 函数y=$\frac{1}{4}$•2x和y=$\frac{1}{3}$x2的图象如图所示,其中有且只有x=x1、x2、x3时,两函数值相等,且x1<0<x2<x3,O为坐标原点.
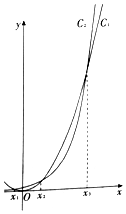
函数y=$\frac{1}{4}$•2x和y=$\frac{1}{3}$x2的图象如图所示,其中有且只有x=x1、x2、x3时,两函数值相等,且x1<0<x2<x3,O为坐标原点.(Ⅰ)请指出图中曲线C1、C2分别对应的函数;
(Ⅱ)请判断以下两个结论是否正确,并说明理由.
①当x∈(-∞,-1)时,$\frac{1}{4}$•2x<$\frac{1}{3}$x2;
②x2∈(1,2).
分析 (Ⅰ)根据二次函数和指数型函数的图象和性质,可得曲线C1、C2分别对应的函数;
(Ⅱ)根据函数图象,数形结合,可得两个结论的正误.
解答 解:(Ⅰ)y=$\frac{1}{3}$x2是二次函数,故与图中C1对应;
函数y=$\frac{1}{4}$•2x是指数型函数,故与图中C2对应;
(Ⅱ)当x=-1时,$\frac{1}{4}$•2x<$\frac{1}{3}$x2,
当x=0时,$\frac{1}{4}$•2x>$\frac{1}{3}$x2,
故x1∈(-1,0),
故①当x∈(-∞,-1)时,$\frac{1}{4}$•2x<$\frac{1}{3}$x2正确;
当x=1时,$\frac{1}{4}$•2x>$\frac{1}{3}$x2,
当x=2时,$\frac{1}{4}$•2x<$\frac{1}{3}$x2,
当x=5时,$\frac{1}{4}$•2x<$\frac{1}{3}$x2,
当x=6时,$\frac{1}{4}$•2x>$\frac{1}{3}$x2,
故x2∈(1,2),x3∈(5,6),
故②正确;
点评 本题考查的知识点是二次函数的图象和性质,指数型函数的图象和性质,数形结合思想,难度中档.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
4.数列-1,3,-5,7,-9,…的一个通项公式为( )
| A. | an=2n-1 | B. | an=(-1)n(1-2n) | C. | an=(-1)n(2n-1) | D. | an(-1)n+1(2n-1) |
5.幂函数f(x)=(m2-2m+1)x2m-1在(0,+∞)上为增函数,则实数m的值为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 1或2 |
2.某企业第三年的产量比第一年的产量增加44%,若每年的平均增长率相同(设为x),则以下结论正确的是( )
| A. | x>22% | B. | x<22% | C. | x=22% | D. | 以上都不对 |
9.已知tan($\frac{π}{4}$+α)=$\frac{1}{2}$,则tanα的值为( )
| A. | -$\frac{1}{3}$ | B. | $\frac{1}{3}$ | C. | -$\frac{1}{2}$ | D. | -1 |
6.设向量$\overrightarrow a,\overrightarrow b$满足$|{\overrightarrow a}|=2\sqrt{2},|{\overrightarrow b}|=\sqrt{2}$,且$\overrightarrow a•\overrightarrow b=1$,则$|{\overrightarrow a-2\overrightarrow b}|$=( )
| A. | $2\sqrt{3}$ | B. | 12 | C. | $2\sqrt{2}$ | D. | 8 |
12.已知向量|$\overrightarrow{a}$|=3,$\overrightarrow{a}$•$\overrightarrow{b}$=$\frac{3}{2}$,|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\frac{3\sqrt{6}}{2}$,则向量$\overrightarrow{a}$在$\overrightarrow{b}$上的投影为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 2 |
13.若抛物线y2=2px(p>0)上一点P(2,y0)到其准线的距离为4,则抛物线的标准方程为( )
| A. | y2=2x | B. | y2=4x | C. | y2=6x | D. | y2=8x |