题目内容
 如图,在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=BB1=1,D是A1C的中点.
如图,在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=BB1=1,D是A1C的中点.(Ⅰ)求BD的长;
(Ⅱ)求证:平面ABB1⊥平面BDC.
考点:平面与平面垂直的判定
专题:综合题,空间位置关系与距离
分析:(Ⅰ)取AC的中点O,连接DO,BO,则DO⊥平面ABC,利用勾股定理,即可求BD的长;
(Ⅱ)证明BC⊥平面ABB1,即可证明平面ABB1⊥平面BDC.
(Ⅱ)证明BC⊥平面ABB1,即可证明平面ABB1⊥平面BDC.
解答:
(Ⅰ)解:取AC的中点O,连接DO,BO,则DO⊥平面ABC,
在Rt△BDO中,BO=
,DO=
,∴BD=
=
;
(Ⅱ)证明:∵∠ABC=90°,
∴BC⊥AB,
∵BB1⊥BC,BB1∩AB=B,
∴BC⊥平面ABB1,
∵BC?平面BDC,
∴平面ABB1⊥平面BDC.
在Rt△BDO中,BO=
| ||
| 2 |
| 1 |
| 2 |
|
| ||
| 2 |
(Ⅱ)证明:∵∠ABC=90°,
∴BC⊥AB,
∵BB1⊥BC,BB1∩AB=B,
∴BC⊥平面ABB1,
∵BC?平面BDC,
∴平面ABB1⊥平面BDC.
点评:本题考查平面与平面垂直的判定,考查线面垂直的性质,属于中档题.

练习册系列答案
相关题目


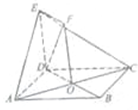 如图,O为正方形ABCD的中心,四边形ODEF是平行四边形,且平面ODEF⊥平面ABCD,AD=2,DE=
如图,O为正方形ABCD的中心,四边形ODEF是平行四边形,且平面ODEF⊥平面ABCD,AD=2,DE=