题目内容
已知函数f(x)=a-bx(b>0)的图象过点A(2,0),B(1,2).
(1)求函数f(x)的解析式;
(2)求f(log481);
(3)解方程f(2x)=-21.
(1)求函数f(x)的解析式;
(2)求f(log481);
(3)解方程f(2x)=-21.
考点:指数函数综合题,指数函数的图像与性质
专题:函数的性质及应用
分析:(1)根据f(x)的图象过点A、B两点,求出b、a的值,得f(x)的解析式;
(2)由f(x)的解析式求出f(log481)的值;
(3)由f(x)的解析式化简方程f(2x)=-21,求出解来即可.
(2)由f(x)的解析式求出f(log481)的值;
(3)由f(x)的解析式化简方程f(2x)=-21,求出解来即可.
解答:
解:(1)∵f(x)=a-bx(b>0)的图象过点A(2,0),B(1,2),
∴
解得b=2,a=4;
∴函数f(x)=4-2x;
(2)∵f(x)=4-2x,
∴f(log481)=4-2log481
=4-2log29
=4-9
=-5;
(3)∵f(x)=4-2x,
∴方程f(2x)=-21可化为
4-22x=-21,
即4+21=22x,
∴22x=25,
∴2x=5,
解得x=log25.
∴
|
|
解得b=2,a=4;
∴函数f(x)=4-2x;
(2)∵f(x)=4-2x,
∴f(log481)=4-2log481
=4-2log29
=4-9
=-5;
(3)∵f(x)=4-2x,
∴方程f(2x)=-21可化为
4-22x=-21,
即4+21=22x,
∴22x=25,
∴2x=5,
解得x=log25.
点评:本题考查了函数的性质的应用问题,也考查了求函数解析式与计算函数值的问题,是综合性题目.

练习册系列答案
相关题目
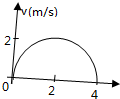 如图所示,一个物体在4s内的速度图象恰好时一个半圆,以下关于物体的运动的说法正确的是( )
如图所示,一个物体在4s内的速度图象恰好时一个半圆,以下关于物体的运动的说法正确的是( )| A、物体前2s作匀加速直线运动,后2s作匀减速直线运动 |
| B、物体在前2s作加速度越来越小的加速运动,后2s作加速度越来越大的减速运动 |
| C、物体在4s内的位移大小是2π(m) |
| D、物体在4s内的位移大小无法确定 |
如图,网格上小正方形的边长为1,粗线画出的是某几何体的三视图,则几何体的表面积为( )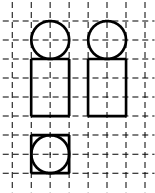

| A、32+4π | ||
| B、24+4π | ||
C、12+
| ||
D、24+
|