题目内容
已知圆C的方程为x2＋(y－4)2＝4，点O是坐标原点．直线l：y＝kx与圆C交于M，N两点．
(1)求k的取值范围；
(2)设Q(m，n)是线段MN上的点，且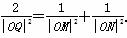
请将n表示为m的函数．
解析：(1)将y＝kx代入x2＋(y－4)2＝4得，
(1＋k2)x2－8kx＋12＝0，(*)
Δ＝(－8k)2－4(1＋k)2×12＞0得k2＞3 .
所以k的取值范围是(－∞，－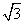
)∪(
，＋∞)．
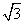(2)因为M、N在直线l上，可设点M、N的坐标分别为(x1，kx1)，(x2，kx2)，则
|OM|2＝(1＋k2)x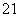
，|ON|2＝(1＋k2)x
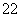，又|OQ|2＝m2＋n2＝(1＋k2)m2,
由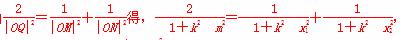
所以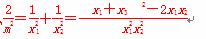
由(*)知x1＋x2＝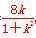
，x1x2＝
，
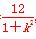所以m2＝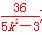
，
因为点Q在直线l上，所以k＝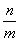
，代入m2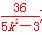＝并化简可得5n2－3m2＝36,
由m2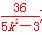＝及k2＞3得0＜m2＜3
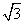，即m∈(－，0)∪(0，).
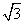依题意，点Q在圆C内，
则n＞0，所以n＝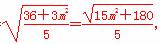
所以，n与m的函数关系为n＝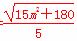
(m∈(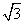－，0)∪(0，))．
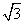练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
＋
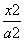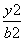＝1(a＞b
＞0)的左焦点为F，离心率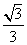
，过点F且与x轴垂直的直线被椭圆截得的线段长为
.
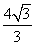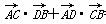＝8，求k的值．
平面ABCD和平面ABEF互相垂直，点M在AC上移动，点N在BF上移动，若CM＝BN＝a(0＜a＜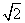
)．
＋
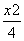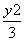＝1的左、右焦点，点P为椭圆C上的动点，则△PF1F2的重心G的轨迹方程为( )
＋
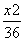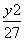＝1(y≠0
) B.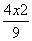
＋y2＝1(y≠0)
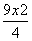＋3y2＝1(y≠0) D．x2＋
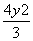＝1(y≠0)
时，切线MA的斜率为－
.
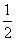，求直线AB的倾斜角α的取值范围．