题目内容
9.函数y=sin($\frac{3π}{4}$-x)sin($\frac{3π}{4}$+x)的值域是[-$\frac{1}{2}$,$\frac{1}{2}$].分析 利用三角函数中的恒等变换应用化简可得函数解析式为y=$\frac{1}{2}$cos2x,根据余弦函数的性质即可得解.
解答 解:∵y=sin($\frac{3π}{4}$-x)sin($\frac{3π}{4}$+x)
=$\frac{\sqrt{2}}{2}$(cosx+sinx)×$\frac{\sqrt{2}}{2}$(cosx-sinx)
=$\frac{1}{2}$(cos2x-sin2x)
=$\frac{1}{2}$cos2x,
又∵cos2x∈[-1,1].
∴y=$\frac{1}{2}$cos2x∈[-$\frac{1}{2}$,$\frac{1}{2}$].
故答案为:[-$\frac{1}{2}$,$\frac{1}{2}$].
点评 本题主要考查了三角函数中的恒等变换应用及余弦函数的图象和性质,属于基础题.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
14.某几何体的三视图如图,则该几何体的表面积为( )
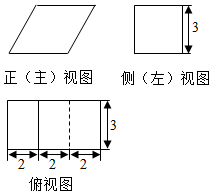

| A. | 48+6$\sqrt{13}$ | B. | 78 | C. | 24+6$\sqrt{13}$ | D. | 68 |
 如图,在△ABC中,∠ACB=90°,CD⊥平面α,AD、BD和平面α所成的角分别为30°和45°,CD=h,求D点到直线AB的距离.
如图,在△ABC中,∠ACB=90°,CD⊥平面α,AD、BD和平面α所成的角分别为30°和45°,CD=h,求D点到直线AB的距离.