题目内容
14．某几何体的三视图如图，则该几何体的表面积为（ ）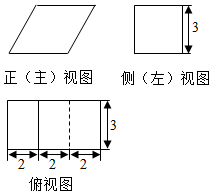
| A． | 48+6$\sqrt{13}$ | B． | 78 | C． | 24+6$\sqrt{13}$ | D． | 68 |
分析 由已知中的三视图可得该几何体是以正（主）视图为底面的柱体，代入柱体表面积公式，可得答案．
解答 解：由已知中的三视图可得该几何体是以正（主）视图为底面的柱体，
柱体的底面面积为：（2+2）×3=12，
底面的周长为：（2+2+$\sqrt{{2}^{2}+{3}^{2}}$）×2=8+2$\sqrt{13}$，
柱体的高为：3，
故柱体的表面积为：S=2×12+3×（8+2$\sqrt{13}$）=48+6$\sqrt{13}$，
故选：A
点评 本题考查的知识点是由三视图，求体积和表面积，根据已知的三视图，判断几何体的形状是解答的关键．
练习册系列答案
海淀黄冈名师导航系列答案
普通高中同步练习册系列答案
相关题目
2．已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的面积是πab，利用这一结论求${∫}_{0}^{\frac{\sqrt{2}}{2}}$$\sqrt{1-2{x}^{2}}$dx等于（ ）
| A． | $\frac{π}{4}$ | B． | $\frac{\sqrt{2}π}{8}$ | C． | $\frac{\sqrt{2}π}{4}$ | D． | $\frac{\sqrt{2}π}{2}$ |
6．已知复数z的实部为2，虚部为1，则（2-i）z=（ ）
| A． | 4+i | B． | 4-i | C． | 5 | D． | 4 |